题目内容
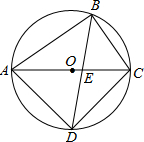 已知四边形ABCD内接于⊙O,AC是直径,BD、AC交于点E,AD=DC.
已知四边形ABCD内接于⊙O,AC是直径,BD、AC交于点E,AD=DC.(1)求证:△ABE∽△DBC;
(2)已知BE•BD=48,
①若tan∠ADB=
| 4 |
| 3 |
②若AD=4
| 6 |
考点:相似三角形的判定与性质,圆周角定理
专题:
分析:(1)证明∠ABE=∠DBC,∠BAE=∠BDC,即可解决问题.
(2)①证明tan∠ACB=tan∠ADB=
=
;证明△ABE∽△DBC,列出比例式
=
,化简求值即可解决问题;
②证明△ADE∽△BDA,得到AD2=BD•DE;结合BE•BD=48,问题即可解决.
(2)①证明tan∠ACB=tan∠ADB=
| AB |
| BC |
| 4 |
| 3 |
| AB |
| BD |
| BE |
| BC |
②证明△ADE∽△BDA,得到AD2=BD•DE;结合BE•BD=48,问题即可解决.
解答: 解:(1)∵AD=DC,
解:(1)∵AD=DC,
∴
=
,
∴∠ABE=∠DBC,而∠BAE=∠BDC,
∴△ABE∽△DBC.
(2)①∵AC为⊙O的直径,
∴∠ABC=90°;
∵∠ADB=∠ACB,
∴tan∠ACB=tan∠ADB=
=
,
设AB=4λ,则BC=3λ;
由勾股定理得AC=5λ;
∵△ABE∽△DBC,
∴
=
,
∴AB•BC=BD•BE=48,
即3λ•4λ=48,
∴λ=2,⊙O的直径=5λ=10.
②∵AD=DC,
∴∠DAE=∠ACD;
又∵∠ABD=∠ACD,
∴∠ABD=∠DAE;
又∵∠ADE=∠BDA,
∴△ADE∽△BDA,
∴
=
,
即AD2=BD•DE,而AD=4
,
∴DE•BD=96,而BE•BD=48,
∴(DE+BE)BD=144,即BD2=144,
∴BD=12.
 解:(1)∵AD=DC,
解:(1)∵AD=DC,∴
 |
| AD |
 |
| DC |
∴∠ABE=∠DBC,而∠BAE=∠BDC,
∴△ABE∽△DBC.
(2)①∵AC为⊙O的直径,
∴∠ABC=90°;
∵∠ADB=∠ACB,
∴tan∠ACB=tan∠ADB=
| AB |
| BC |
| 4 |
| 3 |
设AB=4λ,则BC=3λ;
由勾股定理得AC=5λ;
∵△ABE∽△DBC,
∴
| AB |
| BD |
| BE |
| BC |
∴AB•BC=BD•BE=48,
即3λ•4λ=48,
∴λ=2,⊙O的直径=5λ=10.
②∵AD=DC,
∴∠DAE=∠ACD;
又∵∠ABD=∠ACD,
∴∠ABD=∠DAE;
又∵∠ADE=∠BDA,
∴△ADE∽△BDA,
∴
| AD |
| BD |
| DE |
| AD |
即AD2=BD•DE,而AD=4
| 6 |
∴DE•BD=96,而BE•BD=48,
∴(DE+BE)BD=144,即BD2=144,
∴BD=12.
点评:该题主要考查了圆周角定理、相似三角形的判定及其性质等几何知识点的应用问题;解题的关键是灵活运用有关定理来分析、判断;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
若方程
=
+
有增根,则增根可能为( )
| 5 |
| x-2 |
| a |
| x |
| 4 |
| x(x-2) |
| A、0 | B、2 | C、0或2 | D、1 |
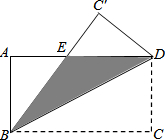 如图,在矩形ABCD中,AB=3,AD=5,现将该矩形沿对角线BD折叠,使得点C落在点C′处,BC′边交AD边于点E,请求出图中阴影部分的面积.
如图,在矩形ABCD中,AB=3,AD=5,现将该矩形沿对角线BD折叠,使得点C落在点C′处,BC′边交AD边于点E,请求出图中阴影部分的面积.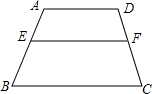 如图,在梯形ABCD中,AD∥BC,EF∥BC,若AD=12cm,BC=17cm,AE:EB=2:3,则EF=
如图,在梯形ABCD中,AD∥BC,EF∥BC,若AD=12cm,BC=17cm,AE:EB=2:3,则EF= 如图所示,已知AB∥A′B′,BC∥B′C′,求证:△OAC∽△OA′C′.
如图所示,已知AB∥A′B′,BC∥B′C′,求证:△OAC∽△OA′C′.