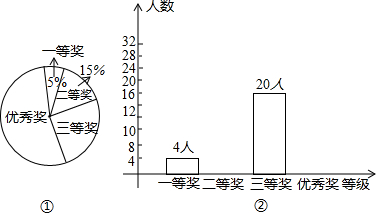
题目内容
8.某超市在端午节前两天每天都花4000元购进咸肉馅和板栗馅粽子若干,已知这两种粽子每个的进价相同,超市第一天咸肉馅粽子以进价的2倍销售,板栗馅粽子提价50%销售,当天全部售完,发现咸肉馅粽子销售了1200个,共获利3200元.(1)设这两种粽子的进价为每个a元,求a的值;
(2)根据前一天的销售情况发现,咸肉馅粽子的数量不能超过板栗馅粽子数量的60%,且按第一天的销售价格销售,求销售利润最多有多少元?
分析 (1)设这两种粽子的进价为每个a元,根据题意列一元一次方程即可;
(2)由(1)知粽子的进价为每个2元,则前两天购进咸肉馅和板栗馅粽子4000÷2=2000个,设利润为W,销售板栗粽子x个,肉馅棕售价4元,板栗粽售价2元,根据题意列出函数表达式,根据咸肉馅粽子的数量不能超过板栗馅粽子数量的60%,得到x的取值范围,利用一次函数性质求最值即可.
解答 解:(1)设这两种粽子的进价为每个a元,则
1.5a×$\frac{4000-1200a}{a}$+1200×2a-4000=3200,
解得:a=2;
(2)由(1)知粽子的进价为每个2元,则前两天每天购进咸肉馅和板栗馅粽子4000÷2=2000个,设利润为W,销售板栗粽子x个,肉馅棕售价4元,板栗粽售价3元,根据题意得:
W=4(2000-x)+3x-4000=-x+4000
∵2000-x≤60%x
∴x≥1250
∵-1<0
∴W随x的增大而减小,
∴当x=1250时,W最大,最大值为W=-1250+4000=2750,
即销售利润最多有2750元.
点评 本题主要考查了一元一次方程的应用和一次函数的应用问题,列出函数表达式根据题意求出x的取值范围再根据一次函数的性质求出最值是本题的难点.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
3. 下面四个所给的选项中,能折成如图给定的图形的是( )
下面四个所给的选项中,能折成如图给定的图形的是( )
 下面四个所给的选项中,能折成如图给定的图形的是( )
下面四个所给的选项中,能折成如图给定的图形的是( )| A. |  | B. |  | C. |  | D. |  |
17.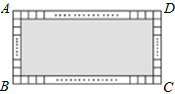 如图,将矩形ABCD分割成1个灰色矩形与148个面积相等的小正方形,若灰色矩形之长与宽的比为5:3,则AD:AB的值是( )
如图,将矩形ABCD分割成1个灰色矩形与148个面积相等的小正方形,若灰色矩形之长与宽的比为5:3,则AD:AB的值是( )
 如图,将矩形ABCD分割成1个灰色矩形与148个面积相等的小正方形,若灰色矩形之长与宽的比为5:3,则AD:AB的值是( )
如图,将矩形ABCD分割成1个灰色矩形与148个面积相等的小正方形,若灰色矩形之长与宽的比为5:3,则AD:AB的值是( )| A. | 5:3 | B. | 11:7 | C. | 23:15 | D. | 47:29 |
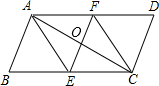 如图,在?ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,分别交BC,AD于点E,F,连接AC,EF相交于点O.若点E是BC的中点,AB⊥AC,AB=2,则四边形AECF的面积是2$\sqrt{3}$.
如图,在?ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,分别交BC,AD于点E,F,连接AC,EF相交于点O.若点E是BC的中点,AB⊥AC,AB=2,则四边形AECF的面积是2$\sqrt{3}$.