题目内容
18.一个正方形的边长为3,则它的对角线长为( )| A. | 3 | B. | 3$\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{6}$ |
分析 首先根据题意画出图形,由正方形的边长为3,可得△ABD是等腰直角三角形,且AD=AB=3,继而求得对角线BD的长.
解答  解:如图,∵四边形ABCD是正方形,
解:如图,∵四边形ABCD是正方形,
∴AD=AB,∠A=90°,
∴△ABD是等腰直角三角形,
∵正方形的边长为3,
∴它的对角线的长为:BD=$\sqrt{A{D}^{2}+B{D}^{2}}$=3$\sqrt{2}$.
故选B.
点评 此题考查了正方形的性质、勾股定理的运用以及等腰直角三角形性质,熟记正方形的各种性质是解题关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
13.0.1252016×(-8)2016的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | $\frac{1}{4}$ |
3. 如图,小明从家到达学校要穿过一个居民小区,小区的道路均是正南或正东方向,则小明走下列线路不能到达学校的是( )
如图,小明从家到达学校要穿过一个居民小区,小区的道路均是正南或正东方向,则小明走下列线路不能到达学校的是( )
 如图,小明从家到达学校要穿过一个居民小区,小区的道路均是正南或正东方向,则小明走下列线路不能到达学校的是( )
如图,小明从家到达学校要穿过一个居民小区,小区的道路均是正南或正东方向,则小明走下列线路不能到达学校的是( )| A. | (0,4)→(0,0)→(4,0) | B. | (0,4)→(4,4)→(4,0) | ||
| C. | (0,4)→(3,4)→(4,2)→(4,0) | D. | (0,4)→(1,4)→(1,1)→(4,1)→(4,0) |
7. 如图所示,正方形ABCD的边长为3,E为CD边上一点,∠DAE=30°,M位AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP长为( )
如图所示,正方形ABCD的边长为3,E为CD边上一点,∠DAE=30°,M位AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP长为( )
 如图所示,正方形ABCD的边长为3,E为CD边上一点,∠DAE=30°,M位AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP长为( )
如图所示,正方形ABCD的边长为3,E为CD边上一点,∠DAE=30°,M位AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP长为( )| A. | 0.5 | B. | 1 | C. | 1或2 | D. | 0.5或2.5 |
8.某商场将一件玩具按进价提高50%后标价,销售时按标价打折销售,结果相对于进价仍获利20%,则这件玩具销售时打的折扣是( )
| A. | 7.5折 | B. | 8折 | C. | 6折 | D. | 3.3折 |
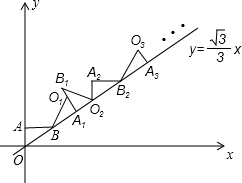 如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y=$\frac{\sqrt{3}}{3}$x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=$\frac{\sqrt{3}}{3}$x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是($\sqrt{3}$,1),则点A8的横坐标是6$\sqrt{3}$+6.
如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y=$\frac{\sqrt{3}}{3}$x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=$\frac{\sqrt{3}}{3}$x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是($\sqrt{3}$,1),则点A8的横坐标是6$\sqrt{3}$+6. 如图是由4个大小相同的小立方块搭成的几何体,这个几何体的俯视图是( )
如图是由4个大小相同的小立方块搭成的几何体,这个几何体的俯视图是( )


