题目内容
12．已知点P是线段MN的黄金分割点，MP＞NP，且MP=（$\sqrt{5}$-1）cm，则NP等于（ ）| A． | 2cm | B． | （3-$\sqrt{5}$）cm | C． | （$\sqrt{5}$-1）cm | D． | （$\sqrt{5}$+1）cm |
分析 根据黄金比值求出MN的长，结合图形计算即可．
解答 解：∵点P是线段MN的黄金分割点，MP＞NP，
∴MP=$\frac{\sqrt{5}-1}{2}$MN，
∴MN=2，
∴NP=MN-MP=（3-$\sqrt{5}$）cm，
故选：B．
点评 本题考查的是黄金分割的概念，把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值$\frac{\sqrt{5}-1}{2}$叫做黄金比．
练习册系列答案
相关题目
3．老师让同学们举一个y是x的函数的例子，同学们分别用表格、图象、函数表达式列举了如下4个x、y之间的关系：
其中y一定是x的函数的是④．（填写所有正确的序号）
①
| ② | ||||||||||
| ③ y=kx+b | ④ y=|x| |
20．
如图，点A在由函数y=（-1）2（x-3n）（x-3n-3）（3n≤x＜3n+3，为自然数）的图象组成的平滑曲线上，点B在x轴上，且AB⊥x轴，若点B从原点O出发，沿x轴向右以每秒1个单位长的速度运动，则第2016秒时，点A的坐标是（ ）
如图，点A在由函数y=（-1）2（x-3n）（x-3n-3）（3n≤x＜3n+3，为自然数）的图象组成的平滑曲线上，点B在x轴上，且AB⊥x轴，若点B从原点O出发，沿x轴向右以每秒1个单位长的速度运动，则第2016秒时，点A的坐标是（ ）| A． | （2016，0） | B． | （2016，2） | C． | （2015，0） | D． | （2016，-2） |
7．下列说法错误的是（ ）
| A． | 48°21′36″的余角是41.64° | |
| B． | 点C是线段AB上的点，AB=10，AC=6，点D是线段BC的中点，则线段CD=2 | |
| C． | ∠AOC=60°，经过顶点O引一条射线OD，且∠AOD=25°，则∠COD=85° | |
| D． | 已知线段a，b如图 ，则尺规作图中 ，线段AD=2a-b |
某工厂接到一批粽子生产任务，按要求在15天内完成，约定这批粽子的出厂价为每只6元，为按时完成任务，该工厂招收了新工人，设新工人王浩第x天生产的粽子数量为y只，y与x满足如下关系：
4．顺次连接四边形ABCD各边的中点，所得四边形是（ ）
| A． | 平行四边形 | B． | 对角线互相垂直的四边形 | ||
| C． | 矩形 | D． | 菱形 |
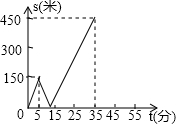甲乙两人匀速从同一地点到1500米处的图书馆看书，甲出发5分钟后，乙以50米/分的速度沿同一路线行走．设甲乙两人相距s（米），甲行走的时间为t（分），s关于t的函数函数图象的一部分如图所示．