题目内容
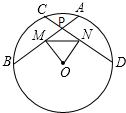 如图,⊙O的两条弦AB、CD相交于点P,M、N分别是AB、CD的中点,PM=PN,求证:AB=CD.
如图,⊙O的两条弦AB、CD相交于点P,M、N分别是AB、CD的中点,PM=PN,求证:AB=CD.考点:垂径定理,勾股定理
专题:证明题
分析:连结OB、OD,如图,根据垂径定理的推论,由M、N分别是AB、CD的中点得到OM⊥AB,ON⊥CD,AM=BM,CN=DN,再由PM=PN得到∠PMN=∠PNM,根据等角的余角相等得∠OMN=∠ONM,则OM=ON,接着根据勾股定理可得BM=DN,于是有AB=CD.
解答:证明:连结OB、OD,如图,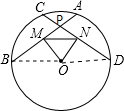
∵M、N分别是AB、CD的中点,
∴OM⊥AB,ON⊥CD,
∴∠OMA=90°,∠ONC=90°,AM=BM,CN=DN,
∵PM=PN,
∴∠PMN=∠PNM,
∴∠OMN=∠ONM,
∴OM=ON,
在Rt△OMB中,BM=
;在Rt△ODN中,DN=
,
而OB=OD,
∴BM=DN,
∴AB=CD.

∵M、N分别是AB、CD的中点,
∴OM⊥AB,ON⊥CD,
∴∠OMA=90°,∠ONC=90°,AM=BM,CN=DN,
∵PM=PN,
∴∠PMN=∠PNM,
∴∠OMN=∠ONM,
∴OM=ON,
在Rt△OMB中,BM=
| OB2-OM2 |
| OD2-ON2 |
而OB=OD,
∴BM=DN,
∴AB=CD.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧;平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.

练习册系列答案
相关题目
若方程ax2+bx+c=0的两个根是-3和1,那么二次函数y=ax2+bx+c的图象的对称轴是直线( )
| A、x=-3 | B、x=-2 |
| C、x=-1 | D、x=1 |
 如图,Rt△ABC中,∠ACB=90°,CD⊥AB,AC=8,AB=10,则AD等于( )
如图,Rt△ABC中,∠ACB=90°,CD⊥AB,AC=8,AB=10,则AD等于( )| A、4.4 | B、5.5 |
| C、6.4 | D、7.4 |
在-3,
,0,3四个数中,最小的数是( )
| 1 |
| 2 |
| A、-3 | ||
B、
| ||
| C、0 | ||
| D、3 |
 如图,MN为半圆O的直径,半径OA⊥MN,C为AM的中点,过点C作BC∥MN交⊙O于点B,求∠NBC的度数.
如图,MN为半圆O的直径,半径OA⊥MN,C为AM的中点,过点C作BC∥MN交⊙O于点B,求∠NBC的度数.