Question

7．如图，以AB为直径的⊙O经过AC的中点D，DE⊥BC于点E．
（1）求证：DE是⊙O的切线；
（2）当AB=4$\sqrt{3}$，∠C=30°时，求图中阴影部分的面积（结果保留根号和π）．

Answer 1

分析 （1）连接OD，利用平行线的判定定理可以得到∠ODE=∠DEC=90°，从而判断DE是圆的切线；
（2）过点O作OF⊥AD，垂足为F，根据等腰三角形的性质得到∠AOD=120°，然后求得阴影部分面积即可．

解答 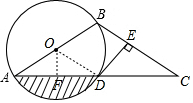解：（1）连接OD，
∵AB是⊙O的直径，D是AC的中点，
∴OD是△ABC的中位线，
∴OD∥BC，
∵DE⊥BC，
∴OD⊥DE，
∵点D在圆上，
∴DE为⊙O的切线；    

（2）过点O作OF⊥AD，垂足为F，
∵OD∥BC，∠C=∠ODF=30°，
∴∠ADO=30°，
∵OD=OA，
∴∠OAD=∠ODA=30°，
∴∠A=∠C，
∴AB=BC=4$\sqrt{3}$，
∴OD=2$\sqrt{3}$，∠AOD=120°，OF=$\sqrt{3}$，
∴AF=3，AD=6，
∴S_△AOD=$\frac{1}{2}$AD•OF=$\frac{1}{2}$×6×$\sqrt{3}$=3$\sqrt{3}$，
∴阴影部分面积S=$\frac{120π•（2\sqrt{3}）^{2}}{360}$-3$\sqrt{3}$=4$π-3\sqrt{3}$．

点评 本题目考查了切线的判定，等腰三角形的判定及性质、圆周角定理及切线的性质，涉及的知识点比较多，解题时候应该注意．