题目内容
8. 已知抛物线y=-x2+bx+c交x轴于C(1,0),D(3,0)两点(点C在点D的左侧),点A为抛物线的顶点.
已知抛物线y=-x2+bx+c交x轴于C(1,0),D(3,0)两点(点C在点D的左侧),点A为抛物线的顶点.(1)求二次函数的解析式;
(2)请在这个二次函数的对称轴上确定一点B,使△ACB是等腰三角形,求出点B的坐标.
分析 (1)把点C和点D的坐标代入抛物线y=-x2+bx+c得出方程组,解方程组即可;
(2)分三种情况:①当BA=BC时;②当AB=AC时;③当CB=CA时;分别得出点B的坐标即可.
解答 解:(1)把C(1,0),D(3,0)代入y=-x2+bx+c得:
$\left\{\begin{array}{l}{-1+b+c=0}\\{-9+3b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=4}\\{c=3}\end{array}\right.$,
∴二次函数的解析式为:y═-x2+4x-3;
(2)∵y═-x2+4x-3=-(x-2)2+1,
∴顶点A的坐标为(2,1),△ACB是等腰三角形,分三种情况: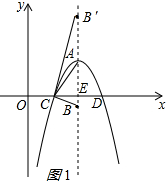
①当BA=BC时,
∵OE=2,OC=1,AE=1,
∴CE=OE-OC=1=AE,△ACE是等腰直角三角形,点B与点E重合,
∴B(2,0);
②当AB=AC时,如图1所示:
∵AC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴AB=$\sqrt{2}$,
∴点B的坐标为(2,1+$\sqrt{2}$)或(2,1-$\sqrt{2}$);
③当CB=CA时,如图2所示: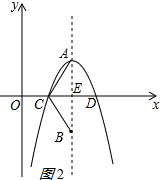
点B与点A关于x轴对称,点B的坐标为(2,-1);
综上所述:△ACB是等腰三角形时,点B的坐标为(2,0)或(2,1+$\sqrt{2}$)或(2,1-$\sqrt{2}$)或(2,-1).
点评 本题考查了二次函数的解析式的求法、等腰三角形的判定、等腰直角三角形的判定、坐标与图形性质、勾股定理等知识;本题综合性强,有一定难度,特别是(2)中,需要进行分类讨论才能得出结果.

练习册系列答案
相关题目
13.用计算器求243,第三个键应按( )
| A. | 4 | B. | 3 | C. | yx | D. | = |
 如图,在△ABC中,AB=AC,AD和BE是高,它们交于点H,且AE=BE.求证:
如图,在△ABC中,AB=AC,AD和BE是高,它们交于点H,且AE=BE.求证: