题目内容
19.用适当的方法解下列方程(1)3x2-10x+6=0
(2)(x-3)2-2(x+1)=x-7.
分析 (1)根据公式法解方程即可;
(2)先把方程化为一般形式,然后利用分解因式法解方程即可.
解答 解:(1)3x2-10x+6=0
∵△=(-10)2-4×3×6=28,
∴x=$\frac{10±\sqrt{28}}{6}$=$\frac{5±\sqrt{7}}{3}$,
∴x1=$\frac{5+\sqrt{7}}{3}$,x2$\frac{5-\sqrt{7}}{3}$,
(2)(x-3)2-2(x+1)=x-7,
化简得:x2-9x+14=0,
(x-2)(x-7)=0,
x-2=0或x-7=0,
解得:x1=2,x2=7.
点评 此题考查了解一元二次方程-因式分解法及公式法,利用因式分解法解方程时,首先将方程右边化为0,左边化为积的形式,由利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程,求出一次方程的解即可得到原方程的解.

练习册系列答案
相关题目
4.在自然数范围内,方程2x+y=7的解有( )
| A. | 一组 | B. | 三组 | C. | 四组 | D. | 无数组 |
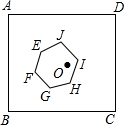 如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个正六边形的边长最大时,AE的最小值为$\frac{\sqrt{2}-1}{2}$.
如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个正六边形的边长最大时,AE的最小值为$\frac{\sqrt{2}-1}{2}$. 如图,菱形ABCD中,AD∥BC,已知BC=CD=5,AC=8,求BD的长.
如图,菱形ABCD中,AD∥BC,已知BC=CD=5,AC=8,求BD的长. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B. 已知抛物线y=-x2+bx+c交x轴于C(1,0),D(3,0)两点(点C在点D的左侧),点A为抛物线的顶点.
已知抛物线y=-x2+bx+c交x轴于C(1,0),D(3,0)两点(点C在点D的左侧),点A为抛物线的顶点.