题目内容
15.如果关于mx2-2(m+2)x+m+5=0没有实数根,那么关于x的方程(m-5)x2-2(m+2)x+m=0的实数根的个数为1或2.分析 由方程mx2-2(m+2)x+m+5=0没有实数根,得△1=4(m+2)2-4m(m+5)<0,解得m>4.关于x的方程(m-5)x2-2(m+2)x+m=0,当m-5=0,为一元一次方程,有一个根;当m-5≠0时,△2=4(m+2)2-4m(m-5)=4(9m+4)>0,有两个不相等的实数根.
解答 解:由方程mx2-2(m+2)x+m+5=0没有实数根,得△1=4(m+2)2-4m(m+5)<0,解得m>4;
关于x的方程(m-5)x2-2(m+2)x+m=0,当m-5=0,为一元一次方程,有一个根;
当m-5≠0时,△2=4(m+2)2-4m(m-5)=4(9m+4),
∵m>4,
∴△2>0,所以方程有两个不相等的实数根.即关于x的方程(m-5)x2-2(m+2)x+m=0的实根的个数为1个或两个.
故答案为:1或2.
点评 本题考查了一元二次方程根的判别式.当△>0,一元二次方程有两个不相等的实根;当△=0,一元二次方程有两个相等的实根;当△<0,一元二次方程没有实根.注意讨论二次项系数,当它不为0,为一元二方程,当它等于0,再看是否为一元一次方程.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
3.若关于x的方程$\frac{{x}^{2}-bx}{ax-c}$=$\frac{m-1}{m+1}$有绝对值相同,符号相反的两个根,则m的值应为( )
| A. | c | B. | $\frac{1}{c}$ | C. | $\frac{a-b}{a+b}$ | D. | $\frac{a+b}{a-b}$ |
4.已知圆O的圆心到直线L的距离为3,若圆上有且只有2个点到L的距离为2,则半径r的取值范围是( )
| A. | r=3 | B. | 1<r<3 | C. | 1<r<5 | D. | 1≤r≤5 |
 如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数. 如图,在Rt△OAB中,∠AOB=30°,AB=2,将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,则AB扫过的面积为π.
如图,在Rt△OAB中,∠AOB=30°,AB=2,将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,则AB扫过的面积为π.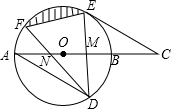 如图,AB是⊙O的直径,弦DE垂直平分半径OB,垂足为M,DE=4,连接AD,过E作AD平行线交AB延长线于点C.
如图,AB是⊙O的直径,弦DE垂直平分半径OB,垂足为M,DE=4,连接AD,过E作AD平行线交AB延长线于点C.