题目内容
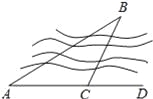
如图，要测量B点到河岸AD的距离，在A点测得∠BAD=30°，在C点测得∠BCD=60°，又测得AC=100米，则B点到河岸AD的距离为（ ）.
A. 100米 B.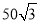 
米 C. 
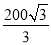米 D. 50米
B
【解析】试题分析：过B作BM⊥AD，根据三角形内角与外角的关系可得∠ABC=30°，再根据等角对等边可得BC=AC=100米，然后再计算出∠CBM=30°，进而得到CM=BC=50米，∴BM=CM=米.
故选：B．
某公司的生产利润原来是a元，经过连续两年的增长达到了y万元，如果每年增长的百分数都是x，那么y与x的函数关系是（）
A. y=x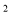
＋a B. y=a（x－1）
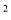C. y=a（1－x）
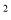D. y=a（1＋x）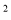
D
【解析】试题分析：根据增长率问题的一般通用公式可得：y=a. 已知二次函数y＝ax2＋bx＋c的图象如图，则下列叙述正确的是( )
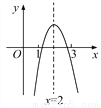
A. abc＜0 B. －3a＋c＜0
C. b2－4ac≥0 D. 将该函数图象向左平移2个单位后所得到抛物线的解析式为y＝ax2＋c
B
【解析】解：A．由开口向下，可得a＜0；又由抛物线与y轴交于负半轴，可得c＜0，然后由对称轴在y轴右侧，得到b与a异号，则可得b＞0，故得abc＞0，故本选项错误；
B．根据图知对称轴为直线x=2，即=2，得b=﹣4a，再根据图象知当x=1时，y=a+b+c=a﹣4a+c=﹣3a+c＜0，故本选项正确；
C．由抛物线与x轴有两个交点，可得b2﹣4ac＞0，故本选项错误；
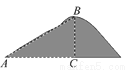
... 如图，某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B，如果AB＝2000米，则他实际上升了________米．
1000
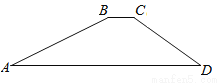
【解析】试题分析：过点B作BC⊥水平面于点C，在Rt△ABC中，根据AB=200米，∠A=30°，求出BC的长度即可．过点B作BC⊥水平面于点C，在Rt△ABC中，∵AB=2000米，∠A=30°，∴BC=ABsin30°=2000×=1000 如图，一水库大坝的横断面为梯形ABCD，坝顶BC宽6米，坝高20米，斜坡AB的坡度i=1：2.5，斜坡CD的坡角为30度，则坝底AD的长度为（ ）
A. 56米 B. 66米 C. （56+20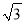
）米 D. （50
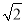+20
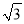）米
C
【解析】试题分析：根据题意可得：BE=CF=20米，根据斜坡AB的坡比为1：2.5可得：AE=50米；根据∠D=30°，CF=20可得：DF=米，则AD=AE+EF+DF=(56+)米，故选C． 已知:如图，二次函数y=a（x﹣h）2+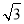
的图象经过原点O（0，0），A（2，0）．
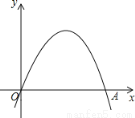
（1）写出该函数图象的对称轴；
（2）若将线段OA绕点O逆时针旋转60°到OA′，试判断点A′是否为该函数图象的顶点？请说明理由.
（1）直线x=1 （2）点A′为抛物线y=﹣（x﹣1）2+的顶点
【解析】
试题分析：（1）把已知点O、A代入函数的解析式可求出h的值h=1，及a=，然后根据二次函数的顶点式的特点判断出对称轴；
（2）由线段OA绕点O逆时针旋转60°到OA′，可知OA′=OA=2，∠A′OA=60°，如图，作A′B⊥x轴于点B，根据直角三角形的特点可知sin60°=，cos60°=,因此可求得A... 若函数y＝3x2的图象与直线y=kx＋3的交点为(2，b)，则k=_____，b＝______.
, 12
【解析】根据题意，把交点坐标（2，b）代入y＝3x2可得b=3×4=12，即交点为（2，12），代入y=kx+3可得k=.
故答案为： ，12. 把多项式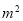
（a﹣2）+m（2﹣a）分解因式等于（ ）.
A．（a﹣2）（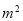
+m） B．（a﹣2）（
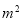﹣m）
C．m（a﹣2）（m﹣1） D．m（a﹣2）（m+1）
C．
【解析】
试题分析：先把（2﹣a）转化为（a﹣2），然后提取公因式m（a﹣2），可得（a﹣2）+m（2﹣a）= m（a﹣2）（m﹣1）.
故选：C． 直角坐标平面上将二次函数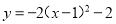
的图象向左平移1个单位，再向上平移1个单位，则其顶点为（ ）
A. （0，0）
B. （1，-2）
C. （0，-1）
D. （-2，1）
C
【解析】由题意得原抛物线的顶点为（1，-2），然后由图象向左平移1个单位，再向上平移1个单位，可得新抛物线的顶点为（0，-1）．
故选：C．