题目内容
若函数y=3x2的图象与直线y=kx+3的交点为(2,b),则k=_____,b=______.
 , 12
【解析】根据题意,把交点坐标(2,b)代入y=3x2可得b=3×4=12,即交点为(2,12),代入y=kx+3可得k=.
故答案为: ,12.
, 12
【解析】根据题意,把交点坐标(2,b)代入y=3x2可得b=3×4=12,即交点为(2,12),代入y=kx+3可得k=.
故答案为: ,12.
练习册系列答案
相关题目
若二次函数y=ax2+bx+c(a≠0)的图象与x轴只有一个交点,则这个交点的坐标是_____.
 (-,0)
【解析】【解析】
∵二次函数y=ax2+bx+c(a≠0)的图象与x轴只有一个交点,∴△=b2-4ac=0,∴,令y=0,解得: .故答案为:(,0).
(-,0)
【解析】【解析】
∵二次函数y=ax2+bx+c(a≠0)的图象与x轴只有一个交点,∴△=b2-4ac=0,∴,令y=0,解得: .故答案为:(,0). 两棵树种在倾角为24°36′的斜坡上,它们的坡面距离是4米,求它们之间的水平距离(可用计算器计算,精确到0.1米)
 3.6米
【解析】试题分析:根据题意可知倾角为24°36′,即坡角为24°36′,
利用余弦关系cos24°36′==0.909,
可求出它们之间的水平距离为:水平距离≈3.6米.
3.6米
【解析】试题分析:根据题意可知倾角为24°36′,即坡角为24°36′,
利用余弦关系cos24°36′==0.909,
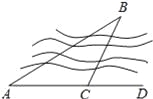
可求出它们之间的水平距离为:水平距离≈3.6米. 如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为( ).
A. 100米 B. 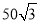 米 C.
米 C. 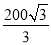 米 D. 50米
米 D. 50米
 B
【解析】试题分析:过B作BM⊥AD,根据三角形内角与外角的关系可得∠ABC=30°,再根据等角对等边可得BC=AC=100米,然后再计算出∠CBM=30°,进而得到CM=BC=50米,∴BM=CM=米.
故选:B.
B
【解析】试题分析:过B作BM⊥AD,根据三角形内角与外角的关系可得∠ABC=30°,再根据等角对等边可得BC=AC=100米,然后再计算出∠CBM=30°,进而得到CM=BC=50米,∴BM=CM=米.
故选:B. 一台机器原价60万元,如果每年的折旧率是x,两年后这台机器的价位约为y万元,求y与x的函数关系式.
 【解析】
试题分析:根据每年的折旧率是x可得一年后的价位为,两年后的价位为.
由题意得y与x的函数关系式为
【解析】
试题分析:根据每年的折旧率是x可得一年后的价位为,两年后的价位为.
由题意得y与x的函数关系式为 下列说法中错误的是( )
A .在函数y=-x2中,当x=0时y有最大值0
B.在函数y=2x2中,当x>0时y随x的增大而增大
C.抛物线y=2x2,y=-x2,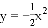 中,抛物线y=2x2的开口最小,抛物线y=-x2的开口最大
中,抛物线y=2x2的开口最小,抛物线y=-x2的开口最大
D.不论a是正数还是负数,抛物线y=ax2的顶点都是坐标原点
 C
【解析】由函数的解析式y=-x2,可知a=-1<0,得到函数的开口向下,有最大值y=0,故A正确;
由函数的解析式y=2x2,可知其对称轴为y轴,对称轴的左边(x<0),y随x增大而减小,对称轴的右边(x>0),y随x增大而增大,故B正确;
根据二次函数的性质,可知系数a决定开口方向和开口大小,且a的值越大开口越小,可知抛物线y=2x2的开口最小,抛物线y=-x2的开口第二小...
C
【解析】由函数的解析式y=-x2,可知a=-1<0,得到函数的开口向下,有最大值y=0,故A正确;
由函数的解析式y=2x2,可知其对称轴为y轴,对称轴的左边(x<0),y随x增大而减小,对称轴的右边(x>0),y随x增大而增大,故B正确;
根据二次函数的性质,可知系数a决定开口方向和开口大小,且a的值越大开口越小,可知抛物线y=2x2的开口最小,抛物线y=-x2的开口第二小... 已知 ,求
,求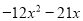 的值.
的值.
 -6
【解析】试题分析:
试题解析:
∵
∴
∴=-3×4x2-21x=-3(2-7x)-21x=-6+21x-21x=-6.
-6
【解析】试题分析:
试题解析:
∵
∴
∴=-3×4x2-21x=-3(2-7x)-21x=-6+21x-21x=-6. 多项式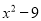 与
与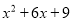 的公因式是
的公因式是
 x+3
【解析】分别将多项式ax2-4a与多项式x2-4x+4进行因式分解,再寻找他们的公因式.
【解析】
∵x2-9=(x-3)(x+3),
x2+6x+9=(x+3)2,
∴多项式x2-9与多项式x2+6x+9的公因式是x+3.
x+3
【解析】分别将多项式ax2-4a与多项式x2-4x+4进行因式分解,再寻找他们的公因式.
【解析】
∵x2-9=(x-3)(x+3),
x2+6x+9=(x+3)2,
∴多项式x2-9与多项式x2+6x+9的公因式是x+3. 函数y=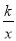 与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A. 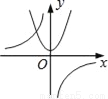 B.
B. 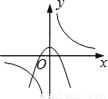 C.
C. 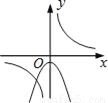 D.
D. 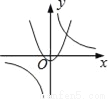
 B
【解析】A选项中,若反比例函数如图,则,那么抛物线应与y轴交于负半轴,所以A不可能;
B选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以B可能;
C选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以C不可能;
D选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以D不可能;
故选B.
...
B
【解析】A选项中,若反比例函数如图,则,那么抛物线应与y轴交于负半轴,所以A不可能;
B选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以B可能;
C选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以C不可能;
D选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以D不可能;
故选B.
... 
