Question

【题目】△ABC和△ECD都是等边三角形，△EBC可以看作是△DAC经过平移、轴对称或旋转得到．

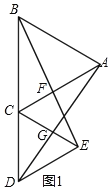
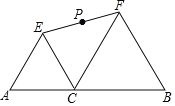
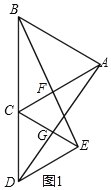
（1）如图1，当B，C，D在同一直线上，AC交BE于点F，AD交CE于点G，求证：CF=CG；

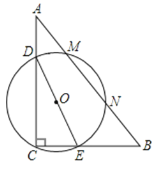
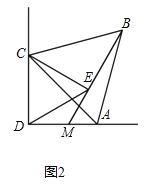
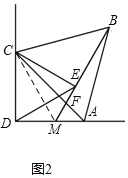
（2）如图2，当△ABC绕点C旋转至AD⊥CD时，连接BE并延长交AD于M，求证：MD=ME．

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】

（1）先根据SAS判定△EBC≌△DAC，得出∠CDA=∠CEB，再根据ASA判定△DCG≌△ECF，即可得出CF=CG；

（2）先根据SAS判定△EBC≌△DAC，得出∠CDA=∠CEB，再连接CM，根据HL判定Rt△CDM≌Rt△CEM，即可得出MD=ME．

（1）如图1．

∵△ABC和△ECD都是等边三角形，∴∠BCA=∠DCE=60°，CD=CE，CA=CB，∴当B，C，D在同一直线上时，∠ACE=60°，∴∠BCE=∠ACD=120°．

在△EBC和△DAC中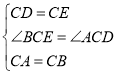，∵，∴△EBC≌△DAC（SAS），∴∠CDA=∠CEB．

在△DCG和△ECF中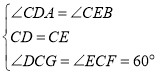，∵，∴△DCG≌△ECF（ASA），∴CF=CG；

（2）连接CM．如图2．

∵△ABC和△ECD都是等边三角形，∴∠BCA=∠DCE=60°，CD=CE，CA=CB，∴∠BCE=∠ACD．

在△EBC和△DAC中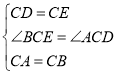，∵，∴△EBC≌△DAC（SAS），∴∠CDA=∠CEB．

∵AD⊥CD，∴∠CEB=∠CDA=90°=∠CEM．

在Rt△CDM和Rt△CEM中，∵，∴Rt△CDM≌Rt△CEM（HL），∴MD=ME．