题目内容
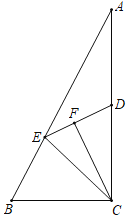
【题目】如图,在![]() 中,
中,![]() ,AC=BC=2,M是边AC的中点,
,AC=BC=2,M是边AC的中点,![]() 于H.
于H.
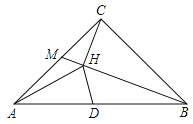
(1)求MH的长度;
(2)求证:![]() ;
;
(3)若D是边AB上的点,且![]() 为等腰三角形,直接写出AD的长.
为等腰三角形,直接写出AD的长.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 或
或![]()
【解析】
(1)根据已知条件M是边AC的中点知![]() ,在直角三角形MBC中利用勾股定理求得
,在直角三角形MBC中利用勾股定理求得![]() ,由同角的余角相等求得
,由同角的余角相等求得![]() ,所以
,所以![]() ,在
,在![]() 中,利用边角关系求得MH的值;
中,利用边角关系求得MH的值;
(2)在![]() 中利用射影定理求得
中利用射影定理求得![]() ,然后结合
,然后结合![]() 即可判定
即可判定![]() ;
;
(3)分三种情况讨论:①AD为底边时;②HD为底边时;③AH为底边时,解直角三角形分别求出AD即可.
解:(1)在![]() 中,
中,![]() ,
,
又∵![]() 是边AC的中点,
是边AC的中点,
∴![]() ,
,
∴![]() ,
,
又![]() 于H,则
于H,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ;
;
(3)∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
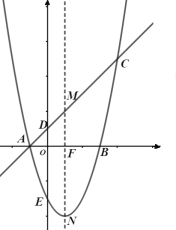
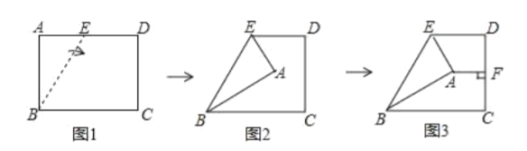
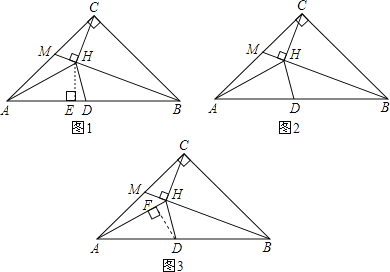
①AD为底边时,如图1,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
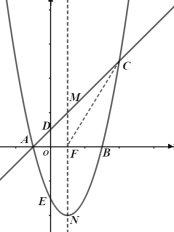
②HD为底边时,如图2,![]() ;
;
③AH为底边时,![]() ,
,
故AD的长为:![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目