题目内容
7．若p是大于5的质数，求（p2+5p+5）2除以120得到的余数．分析 先根据平方差公式添项[（p2+5p+5）2-1]+1再将中括号中的式子分解因式即可得出（p+1）（p+2）（p+3）（p+4），最后判断即可得出结论．
解答 解：∵（p2+5p+5）2=[（p2+5p+5）2-1]+1
=（p2+5p+6）（p2+5p+4）+1
=（p+2）（p+3）（p+1）（p+4）+1
=（p+1）（p+2）（p+3）（p+4）+1，
设M=（p+1）（p+2）（p+3）（p+4），
∵p是大于5的质数，
∴120整除M，
∴（p2+5p+5）2除以120的余数总是1．
点评 此题主要考查了分解因式，整除问题，解本题的关键是给原式减1，再加1，分解成（p+1）（p+2）（p+3）（p+4）+1．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
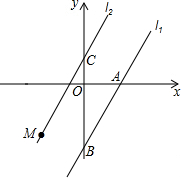如图，一次函数l1：y=2x+b的图象与x轴、y轴分别相交于A、B两点，A的坐标为（2，0），y轴正半轴上有一点C（0，$\frac{3}{2}$），过点C有一条直线l2∥l1（l2与l1的k相等，即k2=k1），M是l2上任意一点．
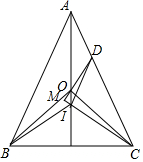△ABC中，AB=AC，O、I分别是其外心、内心，点D在AC上，且DI∥AB，DO的延长线交CI的延长线于M．求证：DM⊥CM．
已知，如图，抛物线y=-x2+bx+c经过直线y=-x+3与坐标轴的两个交点A，B，此抛物线与x轴的另一个交点为C，抛物线的顶点为D．