题目内容
8.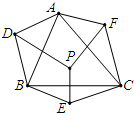 如图,P是△ABC内一点,分别以直线AB,BC,AC为对称轴,作点P的对称点D,E,F.若△ABC的内角∠BAC=70°,∠ABC=60°,∠ACB=50°,则∠DAF+∠DBE+∠ECF等于( )
如图,P是△ABC内一点,分别以直线AB,BC,AC为对称轴,作点P的对称点D,E,F.若△ABC的内角∠BAC=70°,∠ABC=60°,∠ACB=50°,则∠DAF+∠DBE+∠ECF等于( )| A. | 180° | B. | 270° | C. | 360° | D. | 480° |
分析 根据轴对称的性质,可得∠DAB=∠BAP,∠FAC=∠PAC,∠ECB=∠PCB,∠PCA=∠FCA,∠PBA=∠DBA,∠PBC=∠EBC,根据角的和差,可得答案.
解答 解:如图:分别连接AP,BP,CP.
由轴对称的性质,得
∠DAB=∠BAP,∠FAC=∠PAC,∠ECB=∠PCB,∠PCA=∠FCA,∠PBA=∠DBA,∠PBC=∠EBC.
∠DAF+∠DBE+∠ECF=∠DAB+∠BAP+∠FAC+∠PAC+∠ECB+∠PCB+∠PCA+∠FCA+∠PBA+∠DBA+∠PBC+∠EBC
=2(∠BAC+∠ABC+∠BCA)
=2×(70°+60°+50°)
=360°.
故选:C.
点评 本题考查了轴对称的性质,利用轴对称的性质得出∠DAB=∠BAP,∠FAC=∠PAC,∠ECB=∠PCB,∠PCA=∠FCA,∠PBA=∠DBA,∠PBC=∠EBC是解题关键.

练习册系列答案
相关题目
13.一个锐角为52°,则这个角的余角是( )
| A. | 52° | B. | 48° | C. | 128° | D. | 38° |
20.下列方程中,不是一元二次方程的是( )
| A. | 2x2+7=0 | B. | 2x2+2$\sqrt{3}$x+1=0 | C. | 5x2+$\frac{1}{x}$+4=0 | D. | 3x2+(1+x)$\sqrt{2}$+1=0 |
17.下列说法不正确的是( )
| A. | 4的平方根是±2 | B. | -1的立方根是-1 | ||
| C. | $\sqrt{16}$的平方根是±2 | D. | -3是$\sqrt{(-3)^{2}}$的一个平方根 |
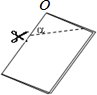 如图把一个矩形的纸片对折两次(折痕互相垂直且交点为O),然后剪下一个角,为了得到一个锐角为50° 的菱形,剪口与折痕所成角α的度数为25°或50°.
如图把一个矩形的纸片对折两次(折痕互相垂直且交点为O),然后剪下一个角,为了得到一个锐角为50° 的菱形,剪口与折痕所成角α的度数为25°或50°.