题目内容
18.若∠A=∠B+∠C,则△ABC是直角三角形.分析 先根据三角形内角定理,可得∠A+∠B+∠C=180°①,再把已知条件∠A=∠B+∠C整体代入①,即可求出∠A=90°,从而得证.
解答 证明:∵在△ABC中,∠A+∠B+∠C=180°,
又∵∠A=∠B+∠C,
∴∠A+∠A=180°,
∴2∠A=180°,
∴∠A=90°,
∴△ABC是直角三角形,
故答案为:直角.
点评 本题利用了三角形内角和定理、整体代入求值、解一元一次方程的知识.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
8.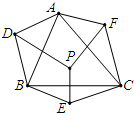 如图,P是△ABC内一点,分别以直线AB,BC,AC为对称轴,作点P的对称点D,E,F.若△ABC的内角∠BAC=70°,∠ABC=60°,∠ACB=50°,则∠DAF+∠DBE+∠ECF等于( )
如图,P是△ABC内一点,分别以直线AB,BC,AC为对称轴,作点P的对称点D,E,F.若△ABC的内角∠BAC=70°,∠ABC=60°,∠ACB=50°,则∠DAF+∠DBE+∠ECF等于( )
 如图,P是△ABC内一点,分别以直线AB,BC,AC为对称轴,作点P的对称点D,E,F.若△ABC的内角∠BAC=70°,∠ABC=60°,∠ACB=50°,则∠DAF+∠DBE+∠ECF等于( )
如图,P是△ABC内一点,分别以直线AB,BC,AC为对称轴,作点P的对称点D,E,F.若△ABC的内角∠BAC=70°,∠ABC=60°,∠ACB=50°,则∠DAF+∠DBE+∠ECF等于( )| A. | 180° | B. | 270° | C. | 360° | D. | 480° |
13.已知三角形的两边长分别为6cm和14cm,则下列长度能作为第三边的是( )
| A. | 12cm | B. | 7cm | C. | 6cm | D. | 25cm |
7.计算(-1)2011+12012应等于( )
| A. | 1 | B. | -2 | C. | -1 | D. | 0 |
 桌子上放着一个圆柱形茶叶盒与一盒餐巾纸(如图所示),你认为它们的俯视图应是( )
桌子上放着一个圆柱形茶叶盒与一盒餐巾纸(如图所示),你认为它们的俯视图应是( )


