题目内容
13.抛物线y=-x2-x+2的顶点坐标是(-$\frac{1}{2}$,$\frac{9}{4}$).分析 已知抛物线的一般式,可以利用顶点坐标公式求解,也可以用配方法求顶点坐标.
解答 解:解法1:利用公式法
y=ax2+bx+c的顶点坐标公式为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),代入数值求得顶点坐标为(-$\frac{1}{2}$,$\frac{9}{4}$).
解法2:利用配方法
y=-x2-x+2=-(x2+x+$\frac{1}{4}$ )+$\frac{9}{4}$=-(x+$\frac{1}{2}$)2+$\frac{9}{4}$,
故顶点的坐标是(-$\frac{1}{2}$,$\frac{9}{4}$).
点评 本题考查了二次函数的性质,熟记公式:y=ax2+bx+c的顶点坐标为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴是x=-$\frac{b}{2a}$是解题的关键.

练习册系列答案
相关题目
3.如图,在平面直角坐标系xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,保持上述运动过程,经过$({2015,\sqrt{3}})$的正六边形的顶点是( )

| A. | C或E | B. | B或D | C. | A或C | D. | B或F |
18. 如图所示的物体是一个实心几何体,其俯视图是( )
如图所示的物体是一个实心几何体,其俯视图是( )
 如图所示的物体是一个实心几何体,其俯视图是( )
如图所示的物体是一个实心几何体,其俯视图是( )| A. |  | B. |  | C. |  | D. |  |
5.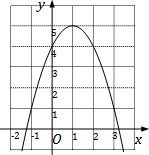 如图是二次函数y=-x2+2x+4的图象,使y≤4成立的x的取值范围是( )
如图是二次函数y=-x2+2x+4的图象,使y≤4成立的x的取值范围是( )
 如图是二次函数y=-x2+2x+4的图象,使y≤4成立的x的取值范围是( )
如图是二次函数y=-x2+2x+4的图象,使y≤4成立的x的取值范围是( )| A. | 0≤x≤2 | B. | x≤0 | C. | x≥2 | D. | x≤0或x≥2 |
2.下列图案中既是轴对称图形又是中心对称图形的是( )
| A. | 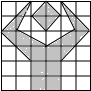 | B. | 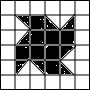 | C. | 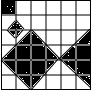 | D. | 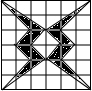 |
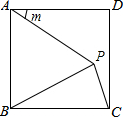 如图,在正方形ABCD中,边AD绕点A顺时针旋转角度m(0°<m<360°),得到线段AP,连接PB,PC.当△BPC是等腰三角形时,m的值为30°或60°或150°或300°.
如图,在正方形ABCD中,边AD绕点A顺时针旋转角度m(0°<m<360°),得到线段AP,连接PB,PC.当△BPC是等腰三角形时,m的值为30°或60°或150°或300°.