题目内容
4.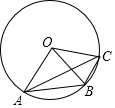 如图,A,B,C是⊙O上三个点,∠AOB=2∠BOC,则下列说法中正确的是( )
如图,A,B,C是⊙O上三个点,∠AOB=2∠BOC,则下列说法中正确的是( )| A. | ∠OBA=∠OCA | B. | 四边形OABC内接于⊙O | ||
| C. | AB=2BC | D. | ∠OBA+∠BOC=90° |
分析 过O作OD⊥AB于D交⊙O于E,由垂径定理得到$\widehat{AE}$=$\widehat{BE}$,于是得到$\widehat{AE}$=$\widehat{BE}$=$\widehat{BC}$,推出AE=BE=BC,根据三角形的三边关系得到2BC>AB,故C错误;根据三角形内角和得到∠OBA=$\frac{1}{2}$(180°-∠AOB)=90°-∠BOC,∠OCA=$\frac{1}{2}$(180°-∠AOC)=90°-$\frac{3}{2}$∠BOC,推出∠OBA≠∠OCA,故A错误;由点A,B,C在⊙O上,而点O在圆心,得到四边形OABC不内接于⊙O,故B错误;根据余角的性质得到∠OBA+∠BOC=90°,故D正确;
解答  解:过O作OD⊥AB于D交⊙O于E,
解:过O作OD⊥AB于D交⊙O于E,
则$\widehat{AE}$=$\widehat{BE}$,
∴AE=BE,∠AOE=∠BOE=$\frac{1}{2}∠$AOB,
∵∠AOB=2∠BOC,
∴∠AOE=∠BOE=∠BOC,
∴$\widehat{AE}$=$\widehat{BE}$=$\widehat{BC}$,
∴AE=BE=BC,
∴2BC>AB,故C错误;
∵OA=OB=OC,
∴∠OBA=$\frac{1}{2}$(180°-∠AOB)=90°-∠BOC,
∠OCA=$\frac{1}{2}$(180°-∠AOC)=90°-$\frac{3}{2}$∠BOC,
∴∠OBA≠∠OCA,故A错误;
∵点A,B,C在⊙O上,而点O在圆心,
∴四边形OABC不内接于⊙O,故B错误;
∵∠BOE=∠BOC=$\frac{1}{2}∠$AOB,
∵∠BOE+∠OBA=90°,
∴∠OBA+∠BOC=90°,故D正确;
故选D.
点评 本题考查了圆心角,弧,弦的关系,垂径定理,三角形的三边关系,正确的作出辅助线是解题的关键.

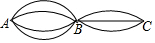 如图,从A地到B地有4条路,从B地到C地也有3条路,则从A地到C地可供选择的方案有( )
如图,从A地到B地有4条路,从B地到C地也有3条路,则从A地到C地可供选择的方案有( )| A. | 3种 | B. | 4种 | C. | 7种 | D. | 12种 |
| 运输工具 | 平均速度(千米/小时) | 运费(元/千米) | 装卸总费用(元) |
| 火车 | 120 | 20 | 2400 |
| 汽车 | 100 | 25 | 1600 |
(2)如果汽车运输总费用比火车运输总费用多1600,求A县与B市之间的路程为多少?
(3)如果小李想将这批水果运往C市销售,选择哪种运输工具比较合算?请说明你的理由.

| A. | ①和② | B. | ②和③ | C. | ①和③ | D. | ②和④ |
 如图,点D,E分别在等边三角形ABC的边BC,AC上,BD=CE.则∠AFE的度数是( )
如图,点D,E分别在等边三角形ABC的边BC,AC上,BD=CE.则∠AFE的度数是( )| A. | 30° | B. | 60° | C. | 72° | D. | 80° |

 如图l1和l2是相交于点O的两条公路,A、B是两个加油站,现准备在∠AOB的内部建一个油库,要求油库的位置点P既到A,B两个加油站的距离相等,又到两条公路l1,l2的距离相等,试用尺规作图作出点P的位置.(不写作法保留作图痕迹)
如图l1和l2是相交于点O的两条公路,A、B是两个加油站,现准备在∠AOB的内部建一个油库,要求油库的位置点P既到A,B两个加油站的距离相等,又到两条公路l1,l2的距离相等,试用尺规作图作出点P的位置.(不写作法保留作图痕迹)