��Ŀ����
15���۲�����ķ�ʽ��-$\frac{2}{{x}^{2}}$��$\frac{5}{{x}^{3}}$��-$\frac{10}{{x}^{4}}$��$\frac{17}{{x}^{5}}$��-$\frac{26}{{x}^{6}}$���������벢̽�����ɣ���9����ʽ��-$\frac{82}{{x}^{10}}$����n����ʽ�ǣ�-1��n$\frac{{n}^{2}+1}{{x}^{n+1}}$������ ��������е�ʽ�ӵķ�ĸΪ��x2��x3��x4��x5��x6���n��ķ�ĸӦΪxn+1�����ӣ�12+1��22+1��32+1�����n��ķ���ӦΪ��n2+1���ɸ����ķ�ʽ���Կ�����������Ϊ����ż����Ϊ�����ɵô𰸣�
��� �⣺�ɷ����ɵõ�9����ʽ�ķ�ĸΪ��x10������Ϊ��92+1������Ϊ�������9����ʽΪ��-$\frac{82}{{x}^{10}}$��
��n����ʽ�ǣ�-1��n$\frac{{n}^{2}+1}{{x}^{n+1}}$��
�ʴ�Ϊ��-$\frac{82}{{x}^{10}}$����-1��n$\frac{{n}^{2}+1}{{x}^{n+1}}$��
���� ���⿼���˷�ʽ�Ķ��壬�����ҹ��ɵ���Ӧ�ù۲�����Щ�����ڱ仯���ܽ�����ֵı仯���ɴӶ��õ�����ʽ�ӵı仯���ɣ�

��ϰ��ϵ�д�
�����Ŀ
6��ij��ij������������8�棬�õ���һ����²���10�棬����������ǣ�������
| A�� | -18�� | B�� | -2�� | C�� | 2�� | D�� | 18�� |
3�����и���������������һ�������εı߳����ǣ�������
| A�� | 3��4��5 | B�� | 1��2��3 | C�� | 4��4��6 | D�� | 5��12��13 |
10����ʽ����$\frac{x}{{x}^{2}-4}$+$\frac{2}{x+2}$=$\frac{1}{x-2}$�ĸ��ǣ�������
| A�� | x=1 | B�� | x=-1 | C�� | x=3 | D�� | x=-3 |
4�������¼��У��������¼��ǣ�������
| A�� | ����ij�Ϧҹ����ѩ | |
| B�� | ��ֻװ�к���Ĵ���������һ������ | |
| C�� | ����˶�Ա���һ�Σ�����10�� | |
| D�� | ������һöӲ�ң����泯�� |
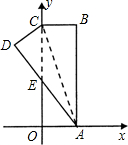 ��ͼ����ֱ������ϵ�У�����ABCO�ı�OA��x���ϣ���OC��y���ϣ���B������Ϊ��1��3�����������ضԽ���AC���ۣ�B������D���λ�ã���AD��y���ڵ�E����˫����$y=\frac{k}{x}$������D����k=-$\frac{48}{25}$��
��ͼ����ֱ������ϵ�У�����ABCO�ı�OA��x���ϣ���OC��y���ϣ���B������Ϊ��1��3�����������ضԽ���AC���ۣ�B������D���λ�ã���AD��y���ڵ�E����˫����$y=\frac{k}{x}$������D����k=-$\frac{48}{25}$��