题目内容
已知等腰△ABC中，AD⊥BC于点D，且AD=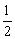
BC，则△ABC底角的度数为( )
A
．45° B．75° C．45°或75° D．60°
C.
详解：根据题意画出图形，注意分别从∠BAC是顶角与∠BAC是底角去分析，然后利用等腰三角形与直角三角形的性质，即可求得答案：
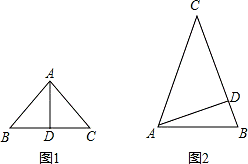
如图1：AB=AC，
∵AD⊥BC，∴BD=CD=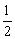BC，∠ADB=90°.
∵AD=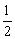BC，∴AD=BD. ∴∠B=45°.
即此时△ABC底角的度数为45°.
如图2，AC=BC，
∵AD⊥BC，∴∠ADC=90°.
∵AD=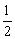BC，∴AD=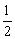AC，∴∠C=30°.∴∠CAB=∠B=(1800－∠A)÷2=75°.
即此时△ABC底角的度数为75°.
综上所述，△ABC底角的度数为45°或75°.故选C.
练习册系列答案
相关题目
九年级（1）班数学活动选出甲、乙两组各10名学生，进行趣味数学答题比赛，共10题，答对题数统计如表一：
（表一）
| 答对题数 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲组 | 1 | 0 | 1 | 5 | 2 | 1 |
| 乙组 | 0 | 0 | 4 | 3 | 2 | 1 |
（表二）
| 平均数 | 众数 | 中位数 | 方差 | |
| 甲组 | 8 | 8 | 8 | 1.6 |
| 乙 | 8 | __________ | __________ | __________ |
（1）根据表一中统计的数据，完成表二；
（2）请你从平均数和方差的角度分析，哪组的成绩更好些？
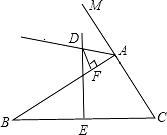
：如图，△ABC中，∠C=90°，学习等边三角形时，我们知道，如果∠A=30°，那么AB=2BC，由此我们猜想，如果AB=2BC，那么∠A=30°，请你利用轴对称变换，证明这个结论．
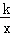与直线y2=﹣x﹣（k+1）在第二象限的交点．AB⊥x轴于B，且S△ABO=
．
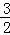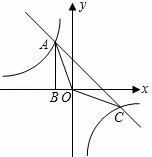（1）求这两个函数的解析式；