题目内容
题面:如图,△ABC的边BC的垂直平分线DE交△BAC的外角平分线AD于D,E为垂足,DF⊥AB于F,且AB>AC,求证:BF=AC+AF.
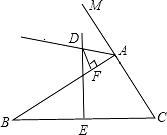
详解:过D作DN⊥AC,垂足为N,连接DB、DC,
则DN=DF(角平分线性质),DB=DC(线段垂直 平分线性质),
平分线性质),
又∵DF⊥AB,DN⊥AC,
∴∠DFB=∠DNC=90°,
在Rt△DBF和Rt△ DCN中
DCN中
∵DB=DC,DF=DN,
∴Rt△DBF≌Rt△DCN(HL)
∴BF=CN,
在Rt△DFA和Rt△DNA中
∵AD=AD,DF=DN,
∴Rt△DFA≌Rt△DNA(HL)
∴AN=AF,
∴BF=AC+AN=AC+AF,
即BF=AF+AC.


练习册系列答案
相关题目
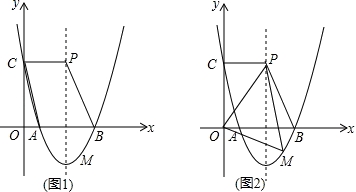

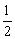 BC,则△ABC底角的度数为( )
BC,则△ABC底角的度数为( ) .45° B.75° C.45°或75° D.60°
.45° B.75° C.45°或75° D.60°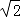 +3
+3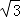 =5
=5 D.
D.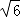 ÷
÷