题目内容
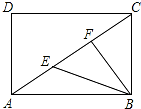
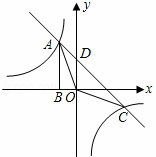
如图,Rt△ABO的顶点A是双曲线y1=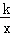 与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=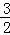 .
.
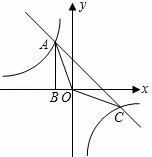 (1)求这两个函数的解析式;
(1)求这两个函数的解析式;
(2)求△AOC的面积.
(3)直接写出使y1>y2成立的x的取值范围
解:(1)设A点坐标为(x,y),且x<0,y>0,
则S△ABO=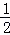 •|BO|•|BA|=
•|BO|•|BA|=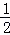 •(﹣x)•y=
•(﹣x)•y=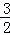 ,
,
∴xy=﹣3, …………………1分
又∵y= ,
,
即xy=k,
∴k=﹣3.
∴所求的两个函数的解析式分别为y=﹣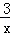 ,y=﹣x+2; …………………3分
,y=﹣x+2; …………………3分
(2)由y=﹣x+2,
令x=0,得y=2.
∴直线y=﹣x+2与y轴的交点D的坐标为(0,2), …………………4分
∵A、C在反比例函数的图象上,
∴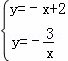 ,解得
,解得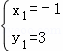 ,
,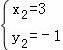 ,
,
∴交点A为(﹣1,3),C为(3,﹣1), …………………6分
∴S△AOC=S△ODA+S△ODC=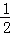 OD•(|x1|+|x2|)=
OD•(|x1|+|x2|)= ×2×(3+1)=4. …………………7分
×2×(3+1)=4. …………………7分
(3)-1<x<0或x>3 (只写对一个不等式给1分) …………………9分

练习册系列答案
相关题目
 BC,则△ABC底角的度数为( )
BC,则△ABC底角的度数为( ) .45° B.75° C.45°或75° D.60°
.45° B.75° C.45°或75° D.60° ,点P在x轴上,则点P的坐标为______;
,点P在x轴上,则点P的坐标为______;
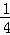 B.
B.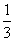 C.
C. 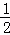 D.
D. 
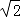 +3
+3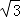 =5
=5 D.
D.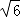 ÷
÷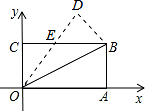
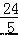 ,
,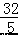 ) D.(
) D.(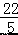 ,
,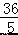 )
)