题目内容
20.有许多代数恒等式可以用图形的面积来表示,如图它表示(2m+n)(m+n)=2m2+3mn+n2.(1)试利用图形的面积来表示(在虚线框内画图):2m2+5mn+2n2并由图形可知该多项式可因式分解为:(2m+n)(m+2n).
(2)小明用8个一样大的矩形(长acm,宽bcm)拼图,拼出了如图的图案:图案是一个大正方形中间留下了边长是2cm的正方形小洞.则(a+2b)2-8ab的值4.

分析 (1)根据多项式的特点、结合题意进行因式分解并画出图形;
(2)结合图形得到答案.
解答  解:(1)2m2+5mn+2n2=(2m+n)(m+2n),
解:(1)2m2+5mn+2n2=(2m+n)(m+2n),
如图所示:
(2)(a+2b)2-8ab=22=4,
故答案为:4.
点评 本题考查的是多项式乘多项式,掌握多项式因式分解的方法、灵活运用数形结合思想是解题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
2.下列运算中,计算正确的是( )
| A. | a3•a2=a6 | B. | a8÷a2=a4 | C. | (ab2)2=a5 | D. | (a2)3=a6 |
5.计算:(-3x2y)•(-2x2y)的结果是( )
| A. | 6x2y | B. | -6x2y | C. | 6x4y2 | D. | -6x4y2 |
10.顺次连结菱形各边中点所得的四边形一定是( )
| A. | 正方形 | B. | 菱形 | C. | 等腰梯形 | D. | 矩形 |
 如图,在Rt△ABC中,∠C=90°,∠A=30°,点P在AC边上,以点P为中心,将△ABC顺时针旋转90°,得到△DEF,DE交边AC于G,当P为中点时,AG:DG的值为$\frac{\sqrt{3}-1}{2}$.
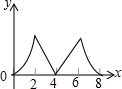
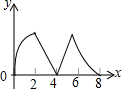
如图,在Rt△ABC中,∠C=90°,∠A=30°,点P在AC边上,以点P为中心,将△ABC顺时针旋转90°,得到△DEF,DE交边AC于G,当P为中点时,AG:DG的值为$\frac{\sqrt{3}-1}{2}$. 如图,正方形ABCD边长为4个单位,两动点P、Q分别从点A、B处,以1单位/s、2单位/s的速度逆时针沿边移动.记移动的时间为x(s),△PBQ面积为y(平方单位),当点Q移动一周又回到点B终止,则y与x的函数关系图象为( )
如图,正方形ABCD边长为4个单位,两动点P、Q分别从点A、B处,以1单位/s、2单位/s的速度逆时针沿边移动.记移动的时间为x(s),△PBQ面积为y(平方单位),当点Q移动一周又回到点B终止,则y与x的函数关系图象为( )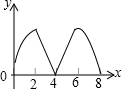

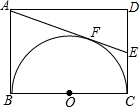 如图所示,在矩形ABCD中,AB=3,BC=4,以BC为直径作半圆O,过点A作半圆O的切线交CD于点E,切点为F,则AE的长为$\frac{13}{3}$.
如图所示,在矩形ABCD中,AB=3,BC=4,以BC为直径作半圆O,过点A作半圆O的切线交CD于点E,切点为F,则AE的长为$\frac{13}{3}$.