��Ŀ����
5�� ���壺������Ϊ$\sqrt{n}$��1��nΪ���������ľ��γ�Ϊ$\sqrt{n}$���Σ����棬����ͨ���۵��ķ�ʽ�۳�һ��$\sqrt{2}$���Σ���ͼ����ʾ��
���壺������Ϊ$\sqrt{n}$��1��nΪ���������ľ��γ�Ϊ$\sqrt{n}$���Σ����棬����ͨ���۵��ķ�ʽ�۳�һ��$\sqrt{2}$���Σ���ͼ����ʾ������1����������ABCD�ع���B��ֱ���۵���ʹ�۵���ĵ�C���ڶԽ���BD�ϵĵ�G�����ۺ�ΪBH��
����2����AD�ع���G��ֱ���۵���ʹ��A����D�ֱ����ڱ�AB��CD�ϣ��ۺ�ΪEF�����ı���BCEFΪ$\sqrt{2}$���Σ�
֤������������ABCD�ı߳�Ϊ1��
��BD=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$��
���۵����ʿ�֪BG=BC=1����AFE=��BFE=90�㣬���ı���BCEFΪ���Σ�
���A=��BFE����EF��AD����$\frac{BG}{BD}$=$\frac{BF}{AB}$����$\frac{1}{\sqrt{2}}$=$\frac{BF}{1}$����BF=$\frac{1}{\sqrt{2}}$��
��BC��BF=1��$\frac{1}{\sqrt{2}}$=$\sqrt{2}��1$�����ı���BCEFΪ$\sqrt{2}$���Σ�
�Ķ��������ݣ��ش��������⣺
��1����ͼ���У�������CH��ȵ��߶���GH��DG��tan��HBC��ֵ��$\sqrt{2}$-1��
��2����֪�ı���BCEFΪ$\sqrt{2}$���Σ�ģ�������������õ��ı���BCMN����ͼ�ڣ���֤���ı���BCMN��$\sqrt{3}$���Σ�
��3����ͼ����$\sqrt{3}$����BCMN���ã�2���еķ�ʽ����3�κõ�һ����$\sqrt{n}$���Ρ�����n��ֵ��
���� ��1�����۵����ɵõ�DG=GH=CH����HC=x������DG=GH=x��DH=$\sqrt{2}$x������DC=DH+CH=1���Ϳ����HC��Ȼ���������Ǻ����Ķ��弴�����tan��HBC��ֵ��
��2��ֻ�����Ķ���֤�����ı���BCEFΪ$\sqrt{2}$���Ρ��ķ����Ϳɽ�����⣻
��3��ͬ��2���е�֤���ɵã���$\sqrt{3}$�������ã�2���еķ�ʽ����1�κõ�һ����$\sqrt{4}$���Ρ�����$\sqrt{4}$�������ã�2���еķ�ʽ����1�κõ�һ����$\sqrt{5}$���Ρ�����$\sqrt{5}$�������ã�2���еķ�ʽ����1�κõ�һ����$\sqrt{6}$���Ρ����ɴ˾Ϳɵõ�n��ֵ��
��� �⣺��1�����۵��ɵã�
DG=HG��GH=CH��
��DG=GH=CH��
��HC=x����DG=GH=x��
�ߡ�DGH=90�㣬
��DH=$\sqrt{2}$x��
��DC=DH+CH=$\sqrt{2}$x+x=1��
���x=$\sqrt{2}$-1��
��tan��HBC=$\frac{HC}{BC}$=$\frac{\sqrt{2}-1}{1}$=$\sqrt{2}$-1��
�ʴ�Ϊ��GH��DG��$\sqrt{2}$-1��
��2����BC=1��EC=BF=$\frac{\sqrt{2}}{2}$��
��BE=$\sqrt{E{C}^{2}+B{C}^{2}}$=$\frac{\sqrt{6}}{2}$��
���۵��ɵ�BP=BC=1����FNM=��BNM=90�㣬��EMN=��CMN=90�㣮
���ı���BCEF�Ǿ��Σ�
���F=��FEC=��C=��FBC=90�㣬
���ı���BCMN�Ǿ��Σ���BNM=��F=90�㣬
��MN��EF��
��$\frac{BP}{BE}$=$\frac{BN}{BF}$����BP•BF=BE•BN��
��1��$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}}{2}$BN��
��BN=$\frac{1}{\sqrt{3}}$��
��BC��BN=1��$\frac{1}{\sqrt{3}}$=$\sqrt{3}$��1��
���ı���BCMN��$\sqrt{3}$�ľ��Σ�
��3��ͬ���ɵã�
��$\sqrt{3}$�������ã�2���еķ�ʽ����1�κõ�һ����$\sqrt{4}$���Ρ���
��$\sqrt{4}$�������ã�2���еķ�ʽ����1�κõ�һ����$\sqrt{5}$���Ρ���
��$\sqrt{5}$�������ã�2���еķ�ʽ����1�κõ�һ����$\sqrt{6}$���Ρ���
���Խ�ͼ���е�$\sqrt{3}$����BCMN���ã�2���еķ�ʽ����3�κõ�һ����$\sqrt{6}$���Ρ���
���� ������Ҫ��������ԳƵ����ʡ������ε����ʡ����ε��ж������ʡ�ƽ���߷��߶γɱ��������ɶ�����֪ʶ���������Ķ�������������������������̽�������������������������о������������������һ�����⣮

| ���� | 13 | 14 | 15 | 16 | 17 | 18 |
| ���� | 4 | 5 | 6 | 6 | 7 | 2 |
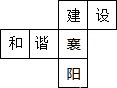 һ���������ƽ��չ��ͼ��ͼ��ʾ�������۳�����������ֶ�������ǣ�������
һ���������ƽ��չ��ͼ��ͼ��ʾ�������۳�����������ֶ�������ǣ�������| A�� | �� | B�� | г | C�� | �� | D�� | �� |
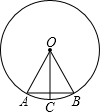 ��ͼ���ڡ�O�У�OA=AB��OC��AB�������н��۴�����ǣ�������
��ͼ���ڡ�O�У�OA=AB��OC��AB�������н��۴�����ǣ�������| A�� | ��OAB�ǵȱ������� | |
| B�� | ��AC�ij�����Բ�ڽ���ʮ�����εı߳� | |
| C�� | OCƽ����AB | |
| D�� | ��BAC=30�� |
| A�� | y=-3��x-1��2 | B�� | y=-3��x+1��2 | C�� | y=-3��x-1��2+2 | D�� | y=-3��x-1��2-2 |
| A�� | a+b=0 | B�� | ab=1 | C�� | a��b=-l | D�� | a��0��b��0 |
 ��ͼ��һ���������ƽ��չ��ͼ����ô��������塰�����ֵĶ�����������ǣ�������
��ͼ��һ���������ƽ��չ��ͼ����ô��������塰�����ֵĶ�����������ǣ�������| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
 ��ͼ��С���ڴ�̨C������ô���AB�Ķ���A������Ϊ45�㣬��ô���AB�ĵײ�B�ĸ���Ϊ30�㣬��֪��̨C�������ľ���CDΪ5m��������ĸ߶�Ϊ5+5$\sqrt{3}$m��������������ţ�
��ͼ��С���ڴ�̨C������ô���AB�Ķ���A������Ϊ45�㣬��ô���AB�ĵײ�B�ĸ���Ϊ30�㣬��֪��̨C�������ľ���CDΪ5m��������ĸ߶�Ϊ5+5$\sqrt{3}$m��������������ţ�