题目内容
12. 已知:如图,在菱形ABCD中,∠BAD=44°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
已知:如图,在菱形ABCD中,∠BAD=44°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )| A. | 112° | B. | 114° | C. | 116° | D. | 118° |
分析 直接利用菱形的性质结合全等三角形的判定与性质得出△DCF≌△BCF(SAS),进而得出∠CDF=∠CBF,再利用垂直平分线的性质得出∠FAB=∠FBA,结合平行线的性质得出∠FBC的度数进而得出答案.
解答  解:连接BF,
解:连接BF,
∵四边形ABCD是菱形,
∴DC=BC,∠1=∠2,∠DAC=∠BAC,
在△DCF和△BCF中
∵$\left\{\begin{array}{l}{DC=BC}\\{∠1=∠2}\\{FC=FC}\end{array}\right.$,
∴△DCF≌△BCF(SAS),
∴∠CDF=∠CBF,
∵EF的垂直平分AB,
∴AF=BF,
∴∠FAB=∠FBA,
∵∠BAD=44°,
∴∠DAC=∠BAC=22°,∠ABC=136°,
∴∠FAB=∠FBA=22°,则∠FBC=136°-22°=114°,
故∠CDF=114°.
故选:B.
点评 此题主要考查了菱形的性质以及全等三角形的判定与性质和线段垂直平分线的性质,正确得出∠CDF=∠CBF是解题关键.

练习册系列答案
相关题目
2.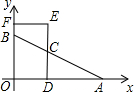 如图,在平面直角坐标系中,点A、B的坐标分别为(4,0)、(0,2),点C为线段AB上任意一点(不与点A、B重合),CD⊥OA于点D,点E在DC的延长线上,EF⊥y轴于点F,若点C为DE的中点,则四边形ODEF的周长为( )
如图,在平面直角坐标系中,点A、B的坐标分别为(4,0)、(0,2),点C为线段AB上任意一点(不与点A、B重合),CD⊥OA于点D,点E在DC的延长线上,EF⊥y轴于点F,若点C为DE的中点,则四边形ODEF的周长为( )
 如图,在平面直角坐标系中,点A、B的坐标分别为(4,0)、(0,2),点C为线段AB上任意一点(不与点A、B重合),CD⊥OA于点D,点E在DC的延长线上,EF⊥y轴于点F,若点C为DE的中点,则四边形ODEF的周长为( )
如图,在平面直角坐标系中,点A、B的坐标分别为(4,0)、(0,2),点C为线段AB上任意一点(不与点A、B重合),CD⊥OA于点D,点E在DC的延长线上,EF⊥y轴于点F,若点C为DE的中点,则四边形ODEF的周长为( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
20.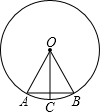 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )
如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )
 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )
如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )| A. | △OAB是等边三角形 | |
| B. | 弦AC的长等于圆内接正十二边形的边长 | |
| C. | OC平分弦AB | |
| D. | ∠BAC=30° |
17.将抛物线y=-3x2-1向右平移1个单位长度,再向上平移1个单位长度后所得的抛物线的解析式为( )
| A. | y=-3(x-1)2 | B. | y=-3(x+1)2 | C. | y=-3(x-1)2+2 | D. | y=-3(x-1)2-2 |
1. 如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB等于( )
如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB等于( )
 如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB等于( )
如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB等于( )| A. | 70° | B. | 20° | C. | 140° | D. | 35° |
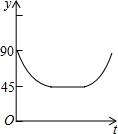
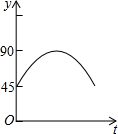
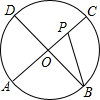 如图,AC、BD为圆O的两条互相垂直的直径,动点P从圆心O出发,沿O→C→D→O的路线在半径OC,劣弧$\widehat{CD}$,半径DO上作匀速运动,设运动时间为t秒,∠APB的度数为y度,那么表示y与t之间函数关系的图象大致为( )
如图,AC、BD为圆O的两条互相垂直的直径,动点P从圆心O出发,沿O→C→D→O的路线在半径OC,劣弧$\widehat{CD}$,半径DO上作匀速运动,设运动时间为t秒,∠APB的度数为y度,那么表示y与t之间函数关系的图象大致为( )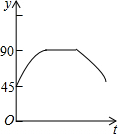

 如图,某电信部门计划修建一条连接B、C两地的电缆,测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200米,电缆BC至少长多少米?($\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414,结果保留整数)
如图,某电信部门计划修建一条连接B、C两地的电缆,测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200米,电缆BC至少长多少米?($\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414,结果保留整数)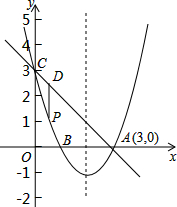 如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与A重合),过点P作PD∥y轴交直线AC于点D.
如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与A重合),过点P作PD∥y轴交直线AC于点D.