Question

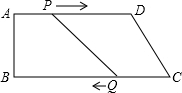如图，在四边形ABCD中，AD∥BC，AD=24cm，BC=26cm．点P从点A出发，以1cm/s的速度向点D运动；点Q从点C同时出发，以3cm/s的速度向点B运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．从运动开始，使PQ∥CD，需经过多少时间？为什么？

Answer 1

考点：平行四边形的判定与性质

专题：动点型

分析：当PQ∥CD，PD∥CQ时，四边形PDCQ为平行四边形，则由“平行四边形的对边相等”得到PD=CQ，由此可以求得点P、Q运动所需要的时间．

解答：解：从运动开始，使PQ∥CD，需经过6s．理由如下：
设从运动开始，使PQ∥CD，需经过ts（0≤t≤

26

3

）．
∵AD∥BC，
∴PD∥QC．
又∵PQ∥CD，
∴四边形PDCQ为平行四边形，
∴PD=CQ，
∵AD=24cm，BC=26cm，
∴24-t=3t，
解得t=6
即从运动开始，使PQ∥CD，需经过6s．

点评：本题考查了平行四边形的判定与性质．解题的关键是了解平行四边形的判定定理，难度不大，但动点问题是个重点知识点．