题目内容
如图，平行四边形ABCD中，∠A的平分线AE交CD于E，AB=5，BC=3，求线段EC的长．考点：平行四边形的性质
专题：
分析：根据平行线的性质以及角平分线的定义证得∠DAE=∠DEA，依据等角对等边，即可求得DE的长，则EC即可求得．
解答：解：∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠DEA=∠EAB，
又∵∠DAE=∠EAB，
∴∠DAE=∠DEA，
∴DE=AD=3，
∴EC=DC-DE=AB-AD=5-3=2．
∴AB∥CD，
∴∠DEA=∠EAB，
又∵∠DAE=∠EAB，
∴∠DAE=∠DEA，
∴DE=AD=3，
∴EC=DC-DE=AB-AD=5-3=2．
点评：本题考查了平行四边形的性质，以及等腰三角形的判定方法，正确证明DE=AD是关键．
练习册系列答案
相关题目
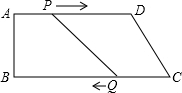如图，在四边形ABCD中，AD∥BC，AD=24cm，BC=26cm．点P从点A出发，以1cm/s的速度向点D运动；点Q从点C同时出发，以3cm/s的速度向点B运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．从运动开始，使PQ∥CD，需经过多少时间？为什么？
如图为一位旅行者从早晨8时出发到郊外所走的路程s（单位：千米）随时间t（单位：时）变化的情况，根据图象回答问题：
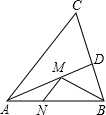选做题：如图，在锐角△ABC中，AB=2，∠BAC=60°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是