题目内容
12．
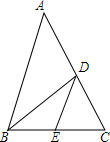如图，在△ABC中，若$\frac{AB}{AD}$=$\frac{BC}{CD}$，AB=9，BC=6，DE∥AB，则△DCE的面积与四边形ABED的面积比是多少？
分析 根据已知条件得到$\frac{CD}{AD}=\frac{6}{9}$=$\frac{2}{3}$，于是得到$\frac{CD}{AC}=\frac{2}{5}$，根据相似三角形的性质得到$\frac{{S}_{△CDE}}{{S}_{△CAB}}$=（$\frac{CD}{AD}$）2=$\frac{4}{25}$，于是得到结论．
解答 解：∵$\frac{AB}{AD}$=$\frac{BC}{CD}$，
∴$\frac{BC}{AB}=\frac{CD}{AD}$，
∵AB=9，BC=6，
∴$\frac{CD}{AD}=\frac{6}{9}$=$\frac{2}{3}$，
∴$\frac{CD}{AC}=\frac{2}{5}$，
∵DE∥AB，
∴△CDE∽△CAB，
∴$\frac{{S}_{△CDE}}{{S}_{△CAB}}$=（$\frac{CD}{AD}$）2=$\frac{4}{25}$，
∴$\frac{{S}_{△CDE}}{{S}_{四边形ABED}}$=$\frac{4}{21}$．
点评 本题考查了相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．
练习册系列答案
相关题目
5．下列判断正确的是（ ）
| A． | 方程是等式，等式就是方程 | B． | 方程是含有未知数的等式 | ||
| C． | 方程的解就是方程的根 | D． | 方程2x=3x没解 |
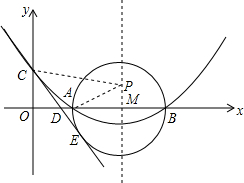如图，已知抛物线的对称轴为直线l：x=4，且与x轴交于点A（2，0），与y轴交于点C（0，2）．
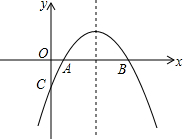如图抛物线y=-x2+bx+c与x轴的两个交点别为A（1，0），B（3，0）
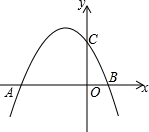如图，抛物线y=-$\frac{3}{8}{x}^{2}-\frac{3}{4}x+3$与x轴交于A，B两点，与y轴交于点C．
已知：AC平分∠DAB，∠DAB+∠DCB=180°，若CE：CB=5：6，则S△ABD：S△CDB=$\frac{11}{25}$．
抛物线y=ax2+b+c的部分图象如图所示，则当y＜0时，x的取值范围是x＜-1或x＞3．