题目内容
2．下列运算中，正确的是（ ）| A． | x+x=x2 | B． | x2•x3=x6 | C． | （x2）3=x6 | D． | （x-y）2=x2-y2 |
分析 分别利用合并同类项法则以及同底数幂的乘法运算法则和幂的乘方运算和完全平方公式化简求出即可．
解答 解：A、x+x=2x，故此选项错误；
B、x2•x3=x5，故此选项错误；
C、（x2）3=x6，故此选项正确；
D、（x-y）2=x2-2xy+y2，故此选项错误；
故选：C．
点评 此题主要考查了合并同类项法则以及同底数幂的乘法运算和幂的乘方运算和完全平方公式等知识，熟练掌握相关运算法则是解题关键．
练习册系列答案
相关题目
12．下列性质中，正方形具有而菱形不一定具有的性质是（ ）
| A． | 四条边相等 | B． | 对角线互相平分 | C． | 对角线相等 | D． | 对角线互相垂直 |
13．
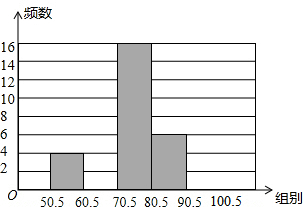青少年“心理健康”问题越来越引起社会的关注，某中学为了了解学校600名学生的心理健康状况，举行了一次“心理健康”知识测试，并随机抽取了部分学生的成绩 （得分取正整数，满分为100分） 作为样本，绘制成如下尚未完成的频数分布表和频数分布直方图．
请根据图表，解答下面的问题：
（1）a=0.32，b=6，c=0.12，d=50；
（2）根据该样本，估计该校本次心理健康知识测试成绩在90分以上的人数；
（3）如果成绩在70分以上为心理健康状况良好，且心理健康状况良好的人数占总人数的70%以上，就表示该校学生的心理健康状况正常，否则就需要加强心理辅导．请根据上述数据分析该校学生是否需要加强心理辅导，并说明理由．
青少年“心理健康”问题越来越引起社会的关注，某中学为了了解学校600名学生的心理健康状况，举行了一次“心理健康”知识测试，并随机抽取了部分学生的成绩 （得分取正整数，满分为100分） 作为样本，绘制成如下尚未完成的频数分布表和频数分布直方图．| 分组 | 频数 | 频率 |
| 50.5～60.5 | 4 | 0.08 |
| 60.5～70.5 | 14 | 0.28 |
| 70.5～80.5 | 16 | a |
| 80.5～90.5 | b | c |
| 90.5～100.5 | 10 | 0.2 |
| 合计 | d | 1.00 |
（1）a=0.32，b=6，c=0.12，d=50；
（2）根据该样本，估计该校本次心理健康知识测试成绩在90分以上的人数；
（3）如果成绩在70分以上为心理健康状况良好，且心理健康状况良好的人数占总人数的70%以上，就表示该校学生的心理健康状况正常，否则就需要加强心理辅导．请根据上述数据分析该校学生是否需要加强心理辅导，并说明理由．
10．下列各对x，y的值中，（ ）不是方程3x+4y=5的解．
| A． | $\left\{{\begin{array}{l}{x=1}\\{y=\frac{1}{2}}\end{array}}\right.$ | B． | $\left\{{\begin{array}{l}{x=-1}\\{y=2}\end{array}}\right.$ | C． | $\left\{{\begin{array}{l}{x=0}\\{y=\frac{5}{4}}\end{array}}\right.$ | D． | $\left\{{\begin{array}{l}{x=\frac{3}{5}}\\{y=0}\end{array}}\right.$ |
某校学生来自甲、乙、丙三个地区，其人数比为2：7：3，如图所示的扇形图表示上述分布情况，则∠AOB=60°．
7．
如图中，利用面积的等量关系验证的公式是（ ）
如图中，利用面积的等量关系验证的公式是（ ）| A． | a2-b2=（a+b）（a-b） | B． | （a-b）2=a2-2ab+b2 | ||
| C． | （a+2b）（a-b）=a2+ab-2b2 | D． | （a+b）2=a2+2ab+b2 |
11．已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=∠A，则此三角形（ ）
| A． | 一定有一个内角为45° | B． | 一定有一个内角为60° | ||
| C． | 一定是直角三角形 | D． | 一定是钝角三角形 |
12．某地区为了进一步缓解交通拥堵问题，决定修建一条长为6千米的公路，如果平均每天的修建费y（万元）与修建天数x（天）之间在30≤x≤120范围内，具有一次函数的关系，如下表所示．
则y关于x的函数解析式为y=-$\frac{1}{5}$x+50（30≤x≤120）．（写出自变量取值范围）
| x | 50 | 60 | 90 | 120 |
| y | 40 | 38 | 32 | 26 |