题目内容
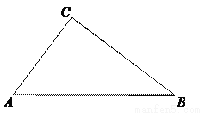
如图,已知在Rt△ABC中,∠ACB=90°,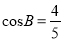 ,BC=8,点D在边BC上,将△ABC沿着过点D的一条直线翻折,使点B落在AB边上的点E处,联结CE、DE,当∠BDE=∠AEC时,则BE的长是 .
,BC=8,点D在边BC上,将△ABC沿着过点D的一条直线翻折,使点B落在AB边上的点E处,联结CE、DE,当∠BDE=∠AEC时,则BE的长是 .
练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
题目内容
如图,已知在Rt△ABC中,∠ACB=90°,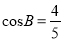 ,BC=8,点D在边BC上,将△ABC沿着过点D的一条直线翻折,使点B落在AB边上的点E处,联结CE、DE,当∠BDE=∠AEC时,则BE的长是 .
,BC=8,点D在边BC上,将△ABC沿着过点D的一条直线翻折,使点B落在AB边上的点E处,联结CE、DE,当∠BDE=∠AEC时,则BE的长是 .

 金博士一点全通系列答案
金博士一点全通系列答案