题目内容
5.一个直角三角形的两边长分别为3,4,则此三角形的外接圆半径是2或$\frac{5}{2}$.分析 直角三角形的外接圆圆心是斜边的中点,那么半径为斜边的一半,分两种情况:①4为斜边长;②3和4为两条直角边长,由勾股定理易求得此直角三角形的斜边长,进而可求得外接圆的半径.
解答 解:由勾股定理可知:
①当直角三角形的斜边长为4,这个三角形的外接圆半径为2;
②当两条直角边长分别为16和12,则直角三角形的斜边长=$\sqrt{{3}^{2}+{4}^{2}}$=5,
因此这个三角形的外接圆半径为$\frac{5}{2}$.
故答案为:2或$\frac{5}{2}$.
点评 本题考查的是直角三角形的外接圆半径,重点在于理解直角三角形的外接圆是以斜边中点为圆心,斜边长的一半为半径的圆.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
15.若点A(-4,y1),B(-1,y2),C(1,y3)在抛物线y=-$\frac{1}{2}$(x+2)2-1上,则( )
| A. | y1<y3<y2 | B. | y2<y1<y3 | C. | y3<y2<y1 | D. | y3<y1<y2 |
20.下列方程为一元二次方程的是( )
| A. | 3x-2=0 | B. | x2-2x-3 | C. | x2-4x-1=0 | D. | xy+1=0 |
17.等腰三角形一腰上的高与另一腰的夹角为40°,则这个等腰三角形的一个底角的度数为( )
| A. | 50° | B. | 80° | C. | 50°或80° | D. | 25°或65° |
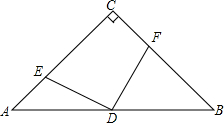 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E在AC上,点F在BC上,且AE=CF.
如图,在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E在AC上,点F在BC上,且AE=CF.


