题目内容
比较a+b与a-b的大小时,我们可以采用下列解法:
解:∵(a+b)-(a-b)=a+b-a+b=2b,
∴当2b>0,即b>0时,a+b>a-b;
当2b<0,即b<0时,a+b<a-b;
当2b=0,即b=0时,a+b=a-b;
这种比较大小的方法叫“作差法”,请用“作差法”比较x2-x+1与x2+2x+1的大小.
解:因为(x2-x+1)-( x2+2x+1)=-3x
所以当-3x>0即x<0时, x2-x+1>x2+2x+1
当-3x<0即x>时, x2-x+1<x2+2x+1
当-3x=0即x=0时, x2-x+1= x2+2x+1

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目





 的解为
的解为 ,则
,则

 得:
得:
 即
即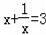
 ,
,




 = 4 ,
= 4 ,
 = 14 ,
= 14 ,
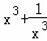
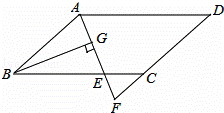
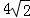 ,则梯形AECD的
,则梯形AECD的