题目内容
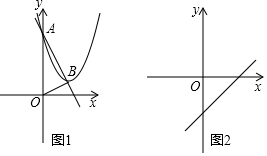
9.在平面直角坐标系中,坐标原点为O,已知抛物线y=a(x-m)2+n与y轴交于点A,它的顶点为点B,则称三角形ABO为抛物线的伴随三角形,直线AB为抛物线的伴随直线.(1)如图1,求抛物线y=(x-2)2+1的伴随直线的解析式;
(2)如图2,若抛物线y=a(x-m)2+n(m>0)的伴随直线是y=x-3,且伴随三角形ABO的面积为3,求此抛物线的解析式.
分析 (1)根据已知条件得到抛物线y=(x-2)2+1与y轴的交点坐标为A(0,5),顶点坐标为B(2,1),列方程组即可得到结论;
(2)根据一次函数的新技术得到伴随直线y=x-3与y轴的交点A(0,-3),得到OA=3,过B作BC⊥y轴于C,根据三角形的面积得到BC=2,得到B(2,-1),把A(0,-3),B(2,-1)代入y=a(x-m)2+n得-3=a(0-2)2-1,即可得到结论.
解答 解:(1)在y=(x-2)2+1,
当x=0时,y=5,
∴抛物线y=(x-2)2+1与y轴的交点坐标为A(0,5),
顶点坐标为B(2,1),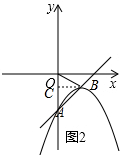
设直线AB的解析式为:y=kx+b,
∴$\left\{\begin{array}{l}{2k+b=1}\\{b=5}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-2}\\{b=5}\end{array}\right.$,
∴抛物线y=(x-2)2+1的伴随直线的解析式为:y=-2x+5;
(2)∵伴随直线y=x-3与y轴的交点A(0,-3),
∴OA=3,
过B作BC⊥y轴于C,
∴$\frac{1}{2}$×3•BC=3,
∴BC=2,
把x=2代入y=x-3得y=-1,
∴B(2,-1),
把A(0,-3),B(2,-1)代入y=a(x-m)2+n得-3=a(0-2)2-1,
∴a=-$\frac{1}{2}$,
∴抛物线的解析式为y=-$\frac{1}{2}$(x-2)2-1.
点评 本题考查了待定系数法求二次函数和一次函数的解析式,三角形的面积的计算,正确的理解题意是解题的关键.

练习册系列答案
相关题目
9.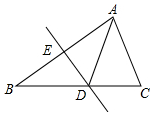 如图,将△ABC沿直线DE折叠后,使得点B与点A重合,已知AC=10cm,△ADC的周长为34cm,则BC的长为( )
如图,将△ABC沿直线DE折叠后,使得点B与点A重合,已知AC=10cm,△ADC的周长为34cm,则BC的长为( )
 如图,将△ABC沿直线DE折叠后,使得点B与点A重合,已知AC=10cm,△ADC的周长为34cm,则BC的长为( )
如图,将△ABC沿直线DE折叠后,使得点B与点A重合,已知AC=10cm,△ADC的周长为34cm,则BC的长为( )| A. | 14cm | B. | 20cm | C. | 44cm | D. | 24cm |
20.在下列多项式乘法运算中,不能运用平方差公式进行运算的是( )
| A. | (2x+3y)(-2x+3y) | B. | (a-2b)(a+2b) | C. | (-x-2y)(x+2y) | D. | (-2x-3y)(3y-2x) |
14.如图,BF、CF分别是∠DBC和∠ECB的角平分线,则关于F的说法不正确的是( )
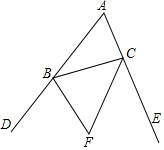

| A. | F到△ABC三边所在直线的距离相等 | B. | F在∠A的平分线上 | ||
| C. | F到△ABC三顶点的距离相等 | D. | F到BD、CE的距离相等 |
18. 将x张长为30厘米、宽为10厘米的长方形白纸按如图所示的方法粘合起来,粘合部分的宽度为2厘米,粘合后的总长度为y厘米,则y关于x的函数关系式是( )
将x张长为30厘米、宽为10厘米的长方形白纸按如图所示的方法粘合起来,粘合部分的宽度为2厘米,粘合后的总长度为y厘米,则y关于x的函数关系式是( )
 将x张长为30厘米、宽为10厘米的长方形白纸按如图所示的方法粘合起来,粘合部分的宽度为2厘米,粘合后的总长度为y厘米,则y关于x的函数关系式是( )
将x张长为30厘米、宽为10厘米的长方形白纸按如图所示的方法粘合起来,粘合部分的宽度为2厘米,粘合后的总长度为y厘米,则y关于x的函数关系式是( )| A. | y=30x | B. | y=28x | C. | y=28x-2 | D. | y=28x+2 |