题目内容
20.梅岭中学数学课外小组利用数轴为学校门口的一条马路设计植树方案如下:第k棵树种植在点xk处,其中x1=1,当k≥2时,xk=xk-1+T($\frac{k-1}{5}$)-T($\frac{k-2}{5}$),T(a)表示非负实数a的整数部分,例如T(2.6)=2,T(0.2)=0.按此方案,第2016棵树种植点x2016为404.分析 根据xk的表达式依次写出x1、x2、…、xk,再相加得:xk=1+T($\frac{k-1}{5}$),把k=2016代入即可.
解答 解:由题意得:x1=1,
x2=x1+T($\frac{1}{5}$)-T($\frac{0}{5}$),
x3=x2+T($\frac{2}{5}$)-T($\frac{1}{5}$),
x4=x3+T($\frac{3}{5}$)-T($\frac{2}{5}$),
…
xk=xk-1+T($\frac{k-1}{5}$)-T($\frac{k-2}{5}$),
∴x1+x2+x3+…+xk=1+${x}_{1}+{x}_{2}+{x}_{3}+…+{x}_{k-1}+T(\frac{k-1}{5})$,
∴xk=1+T($\frac{k-1}{5}$),
当k=2016时,x2016=1+T($\frac{2016-1}{5}$)=1+403=404,
故答案为:404.
点评 本题是数字类的规律题,此类题形式多样,它要求在已有知识的基础上去探究,认真观察、仔细思考,善用联想是解决这类问题的方法;本题主要根据公式依次计算并发现规律.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.下列四组线段中,不能组成一个三角形的是( )
| A. | 6,6,3 | B. | 3,3,6 | C. | 3,3,5 | D. | 6,6,9 |
15.《中国县域经济发展报告(2016)》于2016年9月22日在京发布,启东跻身“全国县域经济综合竞争力100强”,位列第22名,比去年上升了5位;今年前三季度,启东全市实现地区生产总值717亿元,717亿用科学记数法表示为( )
| A. | 7.17×109 | B. | 7.17×1010 | C. | 7.17×1011 | D. | 7.17×1012 |
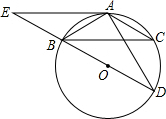 如图,△ABC为⊙O的内接三角形,BD为⊙O的直径,∠ABC=∠D,AC=2$\sqrt{3}$,AD=6,延长DB到E,使BE=BO,连接EA,那么直线EA与⊙O相切吗?为什么?
如图,△ABC为⊙O的内接三角形,BD为⊙O的直径,∠ABC=∠D,AC=2$\sqrt{3}$,AD=6,延长DB到E,使BE=BO,连接EA,那么直线EA与⊙O相切吗?为什么? 如图,已知AB=DC,AC=DB,AC与DB交于点O,求证:OB=OC.
如图,已知AB=DC,AC=DB,AC与DB交于点O,求证:OB=OC.