题目内容
8.圆心角为60°的扇形面积为S,半径为r,则下列图象能大致描述S与r的函数关系的是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据扇形的面积公式S=$\frac{nπ{r}^{2}}{360}$,得出S与r的函数关系式,进而根据函数的性质求解即可.
解答 解:∵圆心角为60°的扇形面积为S,半径为r,
∴S=$\frac{60π{r}^{2}}{360}$=$\frac{π{r}^{2}}{6}$,
∴S是r的二次函数,且r>0,
∴C、D错误;
∵r=1时,S=$\frac{π}{6}$<1;
r=2时,S=$\frac{4π}{6}$≈2.09,
故选A.
点评 本题考查了二次函数的图象与性质,扇形面积的计算,得出S与r的函数关系式是解题的关键.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
17.近几年,我国经济高速发展,但退休人员待遇持续偏低,为了促进社会公平,国家决定大幅增加退休人员退休金,深圳企业退休职工李师傅2014年月退休金为3500元,2016年达到4200元,设李师傅的月退休金从2014年到2016年年平均增长率为x,可列方程为( )
| A. | 3500(1+x)=4200 | B. | 3500(1-x)+3500(1-x)2=4200 | ||
| C. | 3500(1-x)=4200 | D. | 3500(1-x)2=4200 |
19.化简-16(x-$\frac{1}{2}$)的结果是( )
| A. | -16x-$\frac{1}{2}$ | B. | -16x+$\frac{1}{2}$ | C. | -16x-8 | D. | -16x+8 |
13. 如图所示,在⊙O中,OB⊥OC于点O,则∠BAC的度数为( )
如图所示,在⊙O中,OB⊥OC于点O,则∠BAC的度数为( )
 如图所示,在⊙O中,OB⊥OC于点O,则∠BAC的度数为( )
如图所示,在⊙O中,OB⊥OC于点O,则∠BAC的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
20.将直角三角形的各边都缩小或扩大同样的倍数后,得到的三角形( )
| A. | 可能是锐角三角形 | B. | 不可能是直角三角形 | ||
| C. | 仍然是直角三角形 | D. | 可能是钝角三角形 |
17.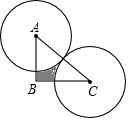 如图,在Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,分别以$\frac{1}{2}$AC的长为半径作圆,将Rt△ABC截去两个扇形,则余下阴影部分的面积为( )cm2.
如图,在Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,分别以$\frac{1}{2}$AC的长为半径作圆,将Rt△ABC截去两个扇形,则余下阴影部分的面积为( )cm2.
 如图,在Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,分别以$\frac{1}{2}$AC的长为半径作圆,将Rt△ABC截去两个扇形,则余下阴影部分的面积为( )cm2.
如图,在Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,分别以$\frac{1}{2}$AC的长为半径作圆,将Rt△ABC截去两个扇形,则余下阴影部分的面积为( )cm2.| A. | $\frac{25}{4}$P | B. | 24-$\frac{5}{4}$P | C. | 24-$\frac{25}{6}$P | D. | 24-$\frac{25}{4}$P |



