题目内容
11.已知等腰三角形的周长为30,腰长为x,底边长y,试写出y与x的函数关系式,并指出x的取值范围.分析 根据已知列方程,化为函数关系式,再根据三角形三边的关系确定x的取值范围即可.
解答 解:∵2x+y=30,
∴y=30-2x,即x<15,
∵两边之和大于第三边,
∴x>7.5,
综上可得7.5<x<15
点评 本题考查了等腰三角形的性质及三角形三边关系,运用方程的思想列出关系式、根据三角形三边关系求得x的取值范围是解答本题的关键.

练习册系列答案
相关题目
1.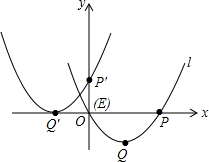 如图,将抛物线l:y=ax2-2x+a2-4(a为常数)向左并向上平移,使顶点Q的对应点Q′,抛物线l与x轴的右交点P的对应点P′分别在两坐标轴上,则抛物线l与x轴的交点E的对应点的坐标为( )
如图,将抛物线l:y=ax2-2x+a2-4(a为常数)向左并向上平移,使顶点Q的对应点Q′,抛物线l与x轴的右交点P的对应点P′分别在两坐标轴上,则抛物线l与x轴的交点E的对应点的坐标为( )
 如图,将抛物线l:y=ax2-2x+a2-4(a为常数)向左并向上平移,使顶点Q的对应点Q′,抛物线l与x轴的右交点P的对应点P′分别在两坐标轴上,则抛物线l与x轴的交点E的对应点的坐标为( )
如图,将抛物线l:y=ax2-2x+a2-4(a为常数)向左并向上平移,使顶点Q的对应点Q′,抛物线l与x轴的右交点P的对应点P′分别在两坐标轴上,则抛物线l与x轴的交点E的对应点的坐标为( )| A. | (-1,$\frac{1}{2}$) | B. | (0,0) | C. | (-$\frac{1}{2}$,1) | D. | (-$\frac{1}{2}$,0) |

 如图,已知△ABC的面积为16,BC=8.现将△ABC沿直线BC向右平移a(a<8)个单位到△DEF的位置.
如图,已知△ABC的面积为16,BC=8.现将△ABC沿直线BC向右平移a(a<8)个单位到△DEF的位置. 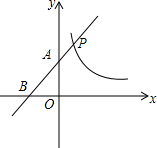 如图,直线y=x+m与双曲线y=$\frac{3}{x}$交于点P,与x轴、y轴交于B、A两点,则PA•PB=6.
如图,直线y=x+m与双曲线y=$\frac{3}{x}$交于点P,与x轴、y轴交于B、A两点,则PA•PB=6. 如图,直线y=$\sqrt{3}$x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A2013的坐标为(22012,0).
如图,直线y=$\sqrt{3}$x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A2013的坐标为(22012,0).