题目内容
3. 靠校园一侧围墙的体育场看台侧面,如图阴影部分所示,看台的三级台阶高度相等,宽度相同,现要用钢管做护栏扶手ACG及三根与水平地面PQ垂直的护栏支架CD、EF和GH(底端D、F、H分别在每级台阶的中点处).已知看台高为1.2米,护栏支架CD=GH=0.8米,∠DCG=66.5°.(参考数据:sin66.5°=0.92,cos66.5°=0.40,tan66.5°=2.30)
靠校园一侧围墙的体育场看台侧面,如图阴影部分所示,看台的三级台阶高度相等,宽度相同,现要用钢管做护栏扶手ACG及三根与水平地面PQ垂直的护栏支架CD、EF和GH(底端D、F、H分别在每级台阶的中点处).已知看台高为1.2米,护栏支架CD=GH=0.8米,∠DCG=66.5°.(参考数据:sin66.5°=0.92,cos66.5°=0.40,tan66.5°=2.30)(1)点D与点H的高度差是0.8米:
(2)试求制作护栏扶手和支架的钢管总长度l,即AC+CG+CD+EF+GH的长度.(结果精确到0.1米)
分析 (1)已知看台由四个台阶组成,由图可看出DH由三个台阶组成,看台的总高度已知,则点D与点H的高度差不难求得;
(2)连接DG,证得DG∥PQ,得出△CDG是直角三角形,根据正弦函数和正切函数求得CG=2,DG=1.84,进一步求得AC=1.84÷4=0.46m,EF=0.8,即可求得制作护栏扶手和支架的钢管总长度.
解答 解:(1)∵看台高为1.2米,看台的三级台阶高度相等,宽度相同,
∴两级台阶高度为0.8米,
∴点D与点H的高度差是0.8米,
故答案为0.8;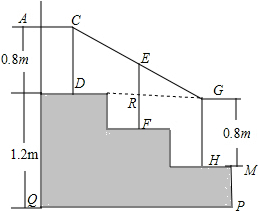
(2)连接DG,
∵点D与点H的高度差是0.8米,GH=0.8m,
∴DG∥PQ,
∴∠CDG=90°,
∴cos∠DCG=$\frac{CD}{CG}$,tan∠DCG=$\frac{DG}{CD}$,
∴CG=$\frac{CD}{cos66.5°}$=$\frac{o.8}{0.4}$=2(m),DG=tan66.5°×0.8=2.3×0.8=1.84(m),
∴AC=1.84÷4=0.46(m),
∵CE=EG,
∴ER=$\frac{1}{2}$CD=0.4m,
∵RF=0.4m,
∴EF=0.8m,
∴AC+CG+CD+EF+GH=0.46+2+0.8×3=4.9(m).
点评 此题主要考查解直角三角形的应用,难度一般,主要要求学生能将实际问题转化为数学模型,然后利用解直角三角形的知识进行解答.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
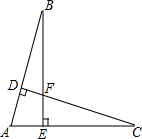 已知AB=AC,CD⊥AB于点D,BE⊥AC于点E,DC、BE相交于点F.求证:BD=CE.
已知AB=AC,CD⊥AB于点D,BE⊥AC于点E,DC、BE相交于点F.求证:BD=CE. 如图,点P是抛物线y=-x2在第四象限内的一点,点A的坐标是(3,0),设点P的坐标是(x,y).
如图,点P是抛物线y=-x2在第四象限内的一点,点A的坐标是(3,0),设点P的坐标是(x,y).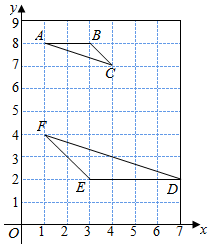 如图,在平面直角坐标系中,每个小方格都是边长为1个单位的小正方形,点A、B、C都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
如图,在平面直角坐标系中,每个小方格都是边长为1个单位的小正方形,点A、B、C都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).