题目内容
3. 如图,A点的坐标是(0,6),AB=BO,∠ABO=120°,C在x轴上运动,在坐标平面内作点D,使AD=DC,∠ADC=120°,连结OD,则OD的长的最小值为$\sqrt{3}$.
如图,A点的坐标是(0,6),AB=BO,∠ABO=120°,C在x轴上运动,在坐标平面内作点D,使AD=DC,∠ADC=120°,连结OD,则OD的长的最小值为$\sqrt{3}$.
分析 先判定△ABO∽△ADC,得出$\frac{AB}{AO}$=$\frac{AD}{AC}$,再根据∠BAD=∠OAC,得出△ACO∽△ADB,进而得到∠ABD=∠AOC=90°,得到当OD⊥BE时,OD最小,最后过O作OF⊥BD于F,根据∠OBF=30°,求得OF=$\frac{1}{2}$OB=$\sqrt{3}$,即OD最小值为$\sqrt{3}$;作B关于y轴的对称点B',则同理可得OD最小值为$\sqrt{3}$.
解答 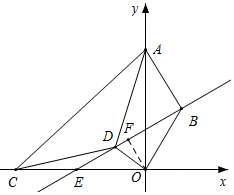 解:如图,作直线BD,由∠DAC=∠DCA=∠BAO=∠BOA=30°,可得△ABO∽△ADC,
解:如图,作直线BD,由∠DAC=∠DCA=∠BAO=∠BOA=30°,可得△ABO∽△ADC,
∴$\frac{AB}{AD}$=$\frac{AO}{AC}$,即$\frac{AB}{AO}$=$\frac{AD}{AC}$,
又∵∠BAD=∠OAC,
∴△ACO∽△ADB,
∴∠ABD=∠AOC=90°,
∵当OD⊥BE时,OD最小,
过O作OF⊥BD于F,则△BOF为Rt△,
∵A点的坐标是(0,6),AB=BO,∠ABO=120°,
∴易得OB=2$\sqrt{3}$,
∵∠ABO=120°,∠ABD=90°,
∴∠OBF=30°,
∴OF=$\frac{1}{2}$OB=$\sqrt{3}$,
即OD最小值为$\sqrt{3}$;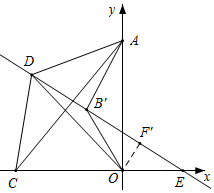
如图,作B关于y轴的对称点B',作直线DB',则同理可得:△ACO∽△ADB',
∴∠AB'D=∠AOC=90°,
∴当OD⊥B'E时,OD最小,
过O作OF'⊥B'D于F',则△B'OF'为Rt△,
∵A点的坐标是(0,6),AB'=B'O,∠AB'O=120°,
∴易得OB'=2$\sqrt{3}$,
∵∠AB'O=120°,∠AB'D=90°,
∴∠OB'F'=30°,
∴OF'=$\frac{1}{2}$OB'=$\sqrt{3}$,
即OD最小值为$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题主要考查了相似三角形的判定与性质、含30°角的直角三角形的性质的综合应用,解决问题的关键是作辅助线,利用垂线段最短进行判断分析.解题时注意:在直角三角形中,30°角所对的直角边等于斜边的一半.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| 与标准质量的差值(单位:g) | -5 | -2 | 0 | 1 | 3 | 6 |
| 袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(2)标准质量为420克,则抽样检测的总质量是多少克.
| A. | 480(1+x)2=270 | B. | 480(1-x)2=270 | C. | 480(1-2x)2=270 | D. | 480(1-x2)=270 |
 如图,长方形OABC的顶点A、C、O都在坐标轴上,点B的坐标为(9,4),E为BC边上一点,CE=6.
如图,长方形OABC的顶点A、C、O都在坐标轴上,点B的坐标为(9,4),E为BC边上一点,CE=6.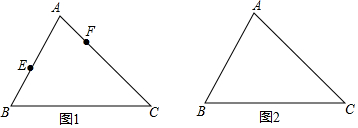
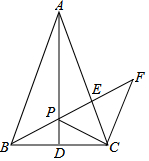 在等腰三角形ABC中,AB=AC,AD⊥BC于点D,CF∥AB,P为AD上一点,连结并延长BP交AC于点E,交CF于点F,求证:
在等腰三角形ABC中,AB=AC,AD⊥BC于点D,CF∥AB,P为AD上一点,连结并延长BP交AC于点E,交CF于点F,求证: