题目内容
 如图,AB是⊙O的直径,延长AB至P,使BP=OB,BD垂直于弦BC,垂足为点B,点D在PC上.设∠PCB=α,∠POC=β.
如图,AB是⊙O的直径,延长AB至P,使BP=OB,BD垂直于弦BC,垂足为点B,点D在PC上.设∠PCB=α,∠POC=β.求证:tanα•tan
| β |
| 2 |
| 1 |
| 3 |
考点:相似三角形的判定与性质,圆周角定理
专题:证明题
分析:连接AC先求出△PBD∽△PAC,再求出
=
,最后得到tanα•tan
=
.
| PB |
| PA |
| 1 |
| 3 |
| β |
| 2 |
| 1 |
| 3 |
解答:证明:连接AC,则∠A=
∠POC=
,

∵AB是⊙O的直径,
∴∠ACB=90°,
∴tanα=
,BD∥AC,
∴∠PBD=∠A,
∵∠P=∠P,
∴△PBD∽△PAC,
∴
=
,
∵PB=0B=OA,
∴
=
,
∴tana•tan
=
•
=
=
.
| 1 |
| 2 |
| β |
| 2 |

∵AB是⊙O的直径,
∴∠ACB=90°,
∴tanα=
| BD |
| BC |
∴∠PBD=∠A,
∵∠P=∠P,
∴△PBD∽△PAC,
∴
| BD |
| AC |
| PB |
| PA |
∵PB=0B=OA,
∴
| PB |
| PA |
| 1 |
| 3 |
∴tana•tan
| β |
| 2 |
| BD |
| BC |
| BC |
| AC |
| BD |
| AC |
| 1 |
| 3 |
点评:本题主要考查了相似三角形的判定与性质及圆周角的知识,本题解题的关键是求出△PBD∽△PAC,再求出tanα•tan
=
.
| β |
| 2 |
| 1 |
| 3 |

练习册系列答案
相关题目

 从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.
从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.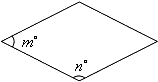 如图,菱形,矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m-n|,于是,|m-n|越小,菱形越接近于正方形.
如图,菱形,矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m-n|,于是,|m-n|越小,菱形越接近于正方形.