题目内容
已知?ABCD的对角线交于点O,M为OD上一点,过点M的直线分别交AD、CD于P、Q两点,与BA、BC的延长线于E、F两点.
(1)如图1,若M为OD的中点,EF∥AC,求证:PE=FQ;
(2)如图2,若M为OD的中点,EF与AC不平行时,求证:PE+FQ=2PQ
(3)如图3,若BM=nDM,EF与AC不平行时,请直接写出:
的值为 .(请用含n的式子表示)

(1)如图1,若M为OD的中点,EF∥AC,求证:PE=FQ;
(2)如图2,若M为OD的中点,EF与AC不平行时,求证:PE+FQ=2PQ
(3)如图3,若BM=nDM,EF与AC不平行时,请直接写出:
| PE+QF |
| PQ |

考点:相似形综合题
专题:
分析:(1)证明△AEP≌△DPQ≌△QCF,即可得到答案.
(2)过O点作ON∥AD交EF于N,则ON是梯形CFPA的中位线,由梯形中位线的性质定理得出AP+CF=2ON,再利用AAS证明△OMN≌△DMP,得出ON=PD,则AP+CF=2PD.然后由CF∥PD,根据平行线分线段成比例定理得出
=
,
=
,将两个式子相加,化简整理后得出QF+PE=2PQ.
(3)若BM=nDM,则有
=
,∴
=
=
,结合(2)即可得到答案.
(2)过O点作ON∥AD交EF于N,则ON是梯形CFPA的中位线,由梯形中位线的性质定理得出AP+CF=2ON,再利用AAS证明△OMN≌△DMP,得出ON=PD,则AP+CF=2PD.然后由CF∥PD,根据平行线分线段成比例定理得出
| QF |
| QP |
| CF |
| PD |
| PE |
| PQ |
| AP |
| PD |
(3)若BM=nDM,则有
| OM |
| DM |
| n-1 |
| 2 |
| ON |
| PD |
| OM |
| DM |
| n-1 |
| 2 |
解答:解:(1)如图1,∵MP∥OA,DM=MO,
∴DP=PA.
在?ABCD中,∵AB∥CD,
∴∠EAP=∠QDP,∠AEP=∠DQP.
在△APE与△DPQ中,
∴△APE≌△DPQ(AAS),
∴PE=PQ.
同理∴△CPQ≌△DPQ,QF=PQ,
∴PE=FQ;

(2)若EF与AC不平行,如图2,过O点作ON∥AD交EF于N,则ON是梯形CFPA的中位线,则AP+CF=2ON.
易证△OMN≌△DMP,
∴ON=PD,
∴AP+CF=2PD.
∵CF∥PD,
我们∴
=
,
∵DQ∥AE,
∴
=
,
∴
+
=
+
,
即:
=
=
=2,
∴PE+FQ=2PQ.

(3)若BM=nDM,则有
=
,∵ON∥PD∴
=
=
,
由(2)知道,
=
=
=n-1
∴
+
=
+
,
∴,
=
=
=n-1.
故答案为n-1.
∴DP=PA.
在?ABCD中,∵AB∥CD,
∴∠EAP=∠QDP,∠AEP=∠DQP.
在△APE与△DPQ中,
|
∴△APE≌△DPQ(AAS),
∴PE=PQ.
同理∴△CPQ≌△DPQ,QF=PQ,
∴PE=FQ;

(2)若EF与AC不平行,如图2,过O点作ON∥AD交EF于N,则ON是梯形CFPA的中位线,则AP+CF=2ON.
易证△OMN≌△DMP,
∴ON=PD,
∴AP+CF=2PD.
∵CF∥PD,
我们∴
| QF |
| QP |
| CF |
| PD |
∵DQ∥AE,
∴
| PE |
| PQ |
| AP |
| PD |
∴
| QF |
| PQ |
| PE |
| PQ |
| CF |
| PD |
| AP |
| PD |
即:
| QF+PE |
| PQ |
| CF+AP |
| PD |
| 2PD |
| PD |
∴PE+FQ=2PQ.

(3)若BM=nDM,则有
| OM |
| DM |
| n-1 |
| 2 |
| ON |
| PD |
| OM |
| DM |
| n-1 |
| 2 |
由(2)知道,
| QF+PE |
| PQ |
| CF+AP |
| PD |
| 2ON |
| PD |
∴
| QF |
| PQ |
| PE |
| PQ |
| CF |
| PD |
| AP |
| PD |
∴,
| QF+PE |
| PQ |
| CF+AP |
| PD |
| 2ON |
| PD |
故答案为n-1.
点评:本题考查了平行四边形的性质,全等三角形的判定与性质,梯形的中位线定理,平行线分线段成比例定理,有一定难度.(2)中正确地作出辅助线,利用平行线分线段成比例定理得出比例式是解题的关键.

练习册系列答案
相关题目
二次根式
中字母x的取值范围是( )
| x-1 |
| A、x<1 | B、x≤1 |
| C、x>1 | D、x≥1 |

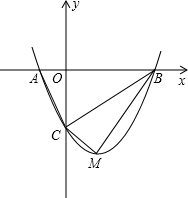 如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点.
如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点. 如图,AB是⊙O的直径,延长AB至P,使BP=OB,BD垂直于弦BC,垂足为点B,点D在PC上.设∠PCB=α,∠POC=β.
如图,AB是⊙O的直径,延长AB至P,使BP=OB,BD垂直于弦BC,垂足为点B,点D在PC上.设∠PCB=α,∠POC=β.