题目内容
8.已知x,y为实数,y=$\frac{\sqrt{{x}^{2}-9}-\sqrt{9-{x}^{2}}+1}{x-3}$,求5x+72y的立方根.分析 根据分式有意义,分母不为0;二次根式的被开方数是非负数列式计算求出x、y的值,根据立方根的概念得到答案.
解答 解:由题意得,x2-9≥0,9-x2≥0,x-3≠0,
解得,x=-3,
则y=-$\frac{1}{6}$,
5x+72y=-27,
∵-27的立方根是-3,
∴5x+72y的立方根是-3.
点评 本题考查的是分式有意义的条件、二次根式有意义的条件和立方根的概念,掌握分式有意义,分母不为0;二次根式的被开方数是非负数是解题的关键.

练习册系列答案
相关题目
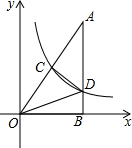 如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=18,则S△OBD的值为12.
如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=18,则S△OBD的值为12. 如图,已知△ABC≌△BAD,AD与BC交于点E,试说明△ABE是等腰三角形.
如图,已知△ABC≌△BAD,AD与BC交于点E,试说明△ABE是等腰三角形.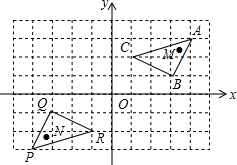 如图,△PQR是三角形ABC经过某种变换后得到的图形.
如图,△PQR是三角形ABC经过某种变换后得到的图形.