题目内容
10．已知b＞a＞0，a2+b2=4ab，则$\frac{a+b}{a-b}$等于-$\sqrt{3}$．分析 利用完全平方公式化简（a+b）2与（a-b）2，把已知等式代入确定出a+b与a-b的值，代入原式计算即可得到结果．
解答 解：∵a2+b2=4ab，
∴（a+b）2=a2+b2+2ab=4ab+2ab=6ab，（a-b）2=a2-2ab+b2=4ab-2ab=2ab，
∵b＞a＞0，
∴a+b=$\sqrt{6ab}$，a-b=-$\sqrt{2ab}$，
则原式=$\frac{\sqrt{6ab}}{-\sqrt{2ab}}$=-$\sqrt{3}$，
故答案为：-$\sqrt{3}$
点评 此题考查了分式的值，以及完全平方公式，熟练掌握公式及法则是解本题的关键．
练习册系列答案
相关题目
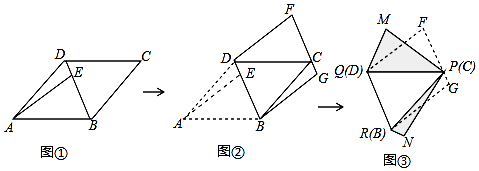
如图，在5×5的网格中，每个小正方形的边长都是1个单位长度，网格中小正方形的顶点叫做格点，矩形ABCD的边分别过格点E，F，G，H，则OD的最大值为6．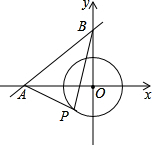
如图，直线y=$\frac{3}{4}$+3与坐标轴交于A、B两点，⊙O的半径为2，点P是⊙O上动点，△ABP面积的最大值为11cm2．