题目内容
8. 如图,AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E作ED⊥AC,垂足为D.直线ED是⊙O的切线吗?为什么?
如图,AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E作ED⊥AC,垂足为D.直线ED是⊙O的切线吗?为什么?
分析 先连接OE,根据等腰三角形的性质和已知条件推出OE∥AD,得∠OED=∠ADE=90°,即可证得ED是圆O的切线..
解答  证明:是,
证明:是,
连接OE,
∵AE平分∠BAC,
∴∠OAE=∠DAE,
∵OA=OE,
∴∠OAE=∠AEO,
∵ED⊥AC,
∴∠ADE=90°,
∴∠EDA+∠DEA=90°,
∴∠OEA+∠AED=90°,即OE⊥ED,
∴ED是圆O的切线.
点评 此题考查的知识点是切线的判定,关键是由已知证得∠OED=90°.

练习册系列答案
相关题目
13.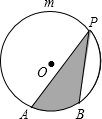 如图,AB是圆内接正六边形的一边,正六边形的半径为2,点P在弧AmB上,点P到直线AB的距离为3,则图中阴影部分的面积为( )
如图,AB是圆内接正六边形的一边,正六边形的半径为2,点P在弧AmB上,点P到直线AB的距离为3,则图中阴影部分的面积为( )
 如图,AB是圆内接正六边形的一边,正六边形的半径为2,点P在弧AmB上,点P到直线AB的距离为3,则图中阴影部分的面积为( )
如图,AB是圆内接正六边形的一边,正六边形的半径为2,点P在弧AmB上,点P到直线AB的距离为3,则图中阴影部分的面积为( )| A. | 3 | B. | $\frac{2π}{3}$ | C. | $\frac{2π}{3}$+3 | D. | $\frac{2π}{3}$-$\sqrt{3}$+3 |
17.已知|a|=4,|b|=2,且a>b,求a+b的值为( )
| A. | 2或6 | B. | -2或6 | C. | ±2 | D. | ±2或±6 |
18.霞浦县处于我国海岸线的中部,有“海滨邹鲁”的美誉,海域面积约为29600平方公里,则数据29600用科学记数法表示为( )
| A. | 2.96×105 | B. | 2.96×104 | C. | 29.6×103 | D. | 2.96×106 |