题目内容
13.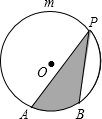 如图,AB是圆内接正六边形的一边,正六边形的半径为2,点P在弧AmB上,点P到直线AB的距离为3,则图中阴影部分的面积为( )
如图,AB是圆内接正六边形的一边,正六边形的半径为2,点P在弧AmB上,点P到直线AB的距离为3,则图中阴影部分的面积为( )| A. | 3 | B. | $\frac{2π}{3}$ | C. | $\frac{2π}{3}$+3 | D. | $\frac{2π}{3}$-$\sqrt{3}$+3 |
分析 由正六边形的性质得出△AOB是等边三角形,得出AB=OA=2,⊙O的半径=2;由三角形的面积公式求出△PAB的面积,弓形AB的面积=扇形AOB的面积-△AOB的面积,即可得出图中阴影部分的面积.
解答 解:连接OA、OB,如图所示: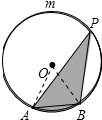
∵AB是圆内接正六边形的一边,
∴∠AOB=60°,
又∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=2,
即⊙O的半径是2;
∵点P到直线AB的距离为3,
∴△PAB的面积=$\frac{1}{2}$×2×3=3,
∵弓形AB的面积=扇形AOB的面积-△AOB的面积=$\frac{60π×{2}^{2}}{360}-\frac{1}{2}×2×\sqrt{3}$=$\frac{2}{3}π-\sqrt{3}$,
∴图中阴影部分的面积=△PAB的面积+弓形AB的面积=$\frac{2}{3}π-\sqrt{3}$+3.
故选:D.
点评 本题考查了正六边形与圆、扇形面积的计算、等边三角形的判定与性质等知识;熟练掌握正六边形的性质,由扇形面积公式求出弓形的面积是解决问题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
3.小明的妈妈在某玩具厂工作,厂里规定每个工人每周要生产某种玩具210个,平均每天生产30个,但由于种种原因,实际每天生产量与计划量相比有出入.下表是小明妈妈某周的生产情况(超产记为正、减产记为负):
(1)根据记录的数据可知小明妈妈星期三生产玩具26个;
(2)根据记录的数据可知小明妈妈本周实际生产玩具217个;
(3)该厂实行“每日计件工资制”.每生产一个玩具可得工资5元,若超额完成任务,则超过部分每个另奖3元;少生产一个则倒扣2元,那么小明妈妈这一周的工资总额是多少元?
(4)若将上面第(3)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,在此方式下小明妈妈这一周的工资与按日计件的工资哪一个更多?请说明理由.
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减产值 | +10 | -12 | -4 | +8 | -1 | +6 | 0 |
(2)根据记录的数据可知小明妈妈本周实际生产玩具217个;
(3)该厂实行“每日计件工资制”.每生产一个玩具可得工资5元,若超额完成任务,则超过部分每个另奖3元;少生产一个则倒扣2元,那么小明妈妈这一周的工资总额是多少元?
(4)若将上面第(3)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,在此方式下小明妈妈这一周的工资与按日计件的工资哪一个更多?请说明理由.
5.一元二次方程x(x-2)=3(x+1)的一般形式是( )
| A. | x2+x+3=0 | B. | x2-3x-3=0 | C. | x2+3x-2=0 | D. | x2-5x-3=0 |
 如图,AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E作ED⊥AC,垂足为D.直线ED是⊙O的切线吗?为什么?
如图,AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E作ED⊥AC,垂足为D.直线ED是⊙O的切线吗?为什么? 如图,四边形ABCD是⊙O的内接四边形,若∠D=100°,则∠ABC的度数是80°.
如图,四边形ABCD是⊙O的内接四边形,若∠D=100°,则∠ABC的度数是80°.