题目内容
 如图是每一个小方格都是边长为1的正方形网格,
如图是每一个小方格都是边长为1的正方形网格,(1)利用网格线作图:
①在BC上找一点P,使点P到AB和AC的距离相等;
②在射线AP上找一点Q,使QB=QC.
(2)在(1)中连接CQ与BQ,试说明CQ⊥BQ.
考点:作图—复杂作图,角平分线的性质,线段垂直平分线的性质
专题:
分析:(1)①根据角平分线的性质得出∠BAC的平分线的位置进而得出答案;
②利用线段垂直平分线的性质得出Q点位置即可;
(2)利用勾股定理的逆定理得出即可.
②利用线段垂直平分线的性质得出Q点位置即可;
(2)利用勾股定理的逆定理得出即可.
解答: 解;(1)①如图所示:P点即为所求;
解;(1)①如图所示:P点即为所求;
②如图所示:Q点即为所求;
(2)∵CQ=
,BQ=
,BC=
,
∴CQ2+BQ2=BC2,
∴CQ⊥BQ.
 解;(1)①如图所示:P点即为所求;
解;(1)①如图所示:P点即为所求;②如图所示:Q点即为所求;
(2)∵CQ=
| 26 |
| 26 |
| 52 |
∴CQ2+BQ2=BC2,
∴CQ⊥BQ.
点评:此题主要考查了线段垂直平分线性质以及角平分线的性质和勾股定理的逆定理,熟练应用相关性质得出是解题关键.

练习册系列答案
相关题目
 已知:点B,C,D在同一直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H,
已知:点B,C,D在同一直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H, 如图,△ABC中,AB=AC,D是BC的中点,试说明AD⊥BC.
如图,△ABC中,AB=AC,D是BC的中点,试说明AD⊥BC.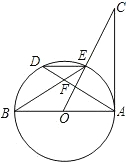 已知:如图,AB是⊙O的直径,AD是弦,OC垂直AD于F交⊙O于E,连接DE、BE,且∠C=∠BED.
已知:如图,AB是⊙O的直径,AD是弦,OC垂直AD于F交⊙O于E,连接DE、BE,且∠C=∠BED. 如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短.
如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短.