题目内容
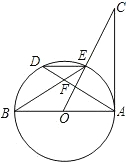 已知:如图,AB是⊙O的直径,AD是弦,OC垂直AD于F交⊙O于E,连接DE、BE,且∠C=∠BED.
已知:如图,AB是⊙O的直径,AD是弦,OC垂直AD于F交⊙O于E,连接DE、BE,且∠C=∠BED.(1)求证:AC是⊙O的切线.
(2)若OA=10,CF=2AF,求AC的长.
考点:切线的判定
专题:
分析:(1)由∠BED=∠BAD,∠C=∠BED,可得∠C=∠AFO,即可证得∠OAC=90°,即可得AC是⊙O的切线.
(2)易证得△ACF∽△OCA,然后由相似三角形的对应边成比例,求得AC的长.
(2)易证得△ACF∽△OCA,然后由相似三角形的对应边成比例,求得AC的长.
解答:(1)证明:∵∠BED=∠BAD,∠C=∠BED,
∴∠BAD=∠C,
∵OC⊥AD,
∴∠BAD+∠AOC=90°,
∴∠C+∠AOC=90°.
∴∠OAC=90°.
∴OA⊥AC.
∴AC是⊙O的切线;
(2)解:∵OA⊥AC,OC⊥AD,
∴∠OAC=∠AFC=90°,
∵∠C是公共角,
∴△ACF∽△OCA,
∴
=
,
∵OA=10,CF=2AF,
∴AC=2OA=20.
∴∠BAD=∠C,
∵OC⊥AD,
∴∠BAD+∠AOC=90°,
∴∠C+∠AOC=90°.
∴∠OAC=90°.
∴OA⊥AC.
∴AC是⊙O的切线;
(2)解:∵OA⊥AC,OC⊥AD,
∴∠OAC=∠AFC=90°,
∵∠C是公共角,
∴△ACF∽△OCA,
∴
| CF |
| AC |
| AF |
| OA |
∵OA=10,CF=2AF,
∴AC=2OA=20.
点评:此题考查了切线的判定以及相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
下列事件中是必然事件的为( )
| A、方程x2-x+1=0有两个不等实根 | ||
B、
| ||
| C、旋转后的图形与原图形的对应线段平行且相等 | ||
| D、圆的切线垂直于圆的半径 |
计算-2×(-3)2-(-3)2×2的结果为( )
| A、0 | B、-54 |
| C、-36 | D、-18 |
 如图是每一个小方格都是边长为1的正方形网格,
如图是每一个小方格都是边长为1的正方形网格,