题目内容
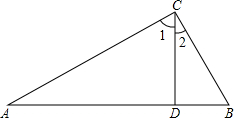 如图,∠ACB=90°,CD⊥AB,垂足为点D,下列结论错误的是( )
如图,∠ACB=90°,CD⊥AB,垂足为点D,下列结论错误的是( )| A、∠A=∠2 |
| B、∠1和∠B都是∠A的余角 |
| C、∠1=∠2 |
| D、图中有3个直角三角形 |
考点:直角三角形的性质,余角和补角
专题:
分析:根据直角三角形两锐角互余和同角的余角相等解答.
解答:解:∵∠ACB=90°,CD⊥AB,
∴∠A+∠1=∠1+∠2=90°,
∴∠A=∠2,
∵∠1+∠A=∠A+∠B=90°,
∴∠1和∠B都是∠A的余角,
直角有∠ACB、∠ADC、∠BDC共3个,
∠1与∠2只有△ABC是等腰直角三角形时相等,
综上所述,错误的结论是∠1=∠2.
故选C.
∴∠A+∠1=∠1+∠2=90°,
∴∠A=∠2,
∵∠1+∠A=∠A+∠B=90°,
∴∠1和∠B都是∠A的余角,
直角有∠ACB、∠ADC、∠BDC共3个,
∠1与∠2只有△ABC是等腰直角三角形时相等,
综上所述,错误的结论是∠1=∠2.
故选C.
点评:本题考查了直角三角形两锐角互余和同角的余角相等的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
下列方程中,是一元二次方程的是( )
A、
| ||
| B、ax2+bx+c=0 | ||
C、x2+
| ||
| D、3x2-2xy-5y2=0 |
等腰三角形的一个角是50°,则它的底角是( )
| A、50° | B、50°或65° |
| C、80° | D、65° |
式子23+23+23+23的计算结果用幂的形式表示正确的是( )
| A、25 |
| B、29 |
| C、212 |
| D、216 |
若x2+xy=-3,xy+y2=5,则x2+2xy+y2的值为( )
| A、2 | B、-2 | C、8 | D、-8 |
 如图,在甲、乙两个4×4的方格图中,每个小正方形的边长都为1.
如图,在甲、乙两个4×4的方格图中,每个小正方形的边长都为1.
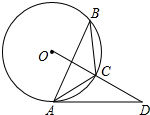 已知:如图,△ABC内接于⊙O,点D在OC的延长线上,∠B=∠CAD=30°.
已知:如图,△ABC内接于⊙O,点D在OC的延长线上,∠B=∠CAD=30°.