题目内容
5.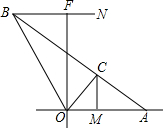 如图,一轮渡从B点出发沿东偏南25°方向匀速航行,经过4.5分钟后达到C处,若保持航线不变,继续航行可直接到达停靠码头A,在停靠码头A的正西反向500m处有一观察站O,在O处测得B位于其北偏西35°,C位于其北偏东55°.求C处到海岸线OA的距离大约是多少米?
如图,一轮渡从B点出发沿东偏南25°方向匀速航行,经过4.5分钟后达到C处,若保持航线不变,继续航行可直接到达停靠码头A,在停靠码头A的正西反向500m处有一观察站O,在O处测得B位于其北偏西35°,C位于其北偏东55°.求C处到海岸线OA的距离大约是多少米?
分析 在Rt△COM中,∠COM=90°-55°=35°,OM=$\frac{CM}{tan35°}$,在Rt△ACM中,∠CAM=25°,AM=$\frac{CM}{tan25°}$,根据OM+AM=AO=500米即可解答.
解答 解:在Rt△COM中,∠COM=90°-55°=35°,
OM=$\frac{CM}{tan35°}$,
在Rt△ACM中,∠CAM=25°,
AM=$\frac{CM}{tan25°}$,
∵OM+AM=AO=500米,
∴$\frac{CM}{tan35°}$+$\frac{CM}{tan25°}$=500,
解得CM=500÷($\frac{1}{tan35°}$+$\frac{1}{tan25°}$)≈500÷($\frac{1}{0.7}$+$\frac{1}{0.466}$)≈139.9米.
点评 本题考查了解直角三角形的应用--方向角问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
相关题目
13.若反比例函数y=$\frac{k}{x}$的图象经过点(2,-2),则k等于( )
| A. | 4 | B. | -4 | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
1.如图,古希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:称图中的数1,5,12,22…为五边形数,则第7个五边形数是( )
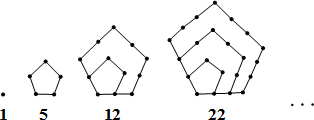

| A. | 62 | B. | 70 | C. | 84 | D. | 108 |
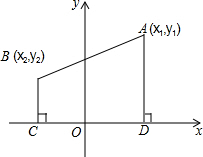 如图,A(x1,y1),B (x2,y2)是直角坐标系中的任意两点,AD,BC都垂直于x轴,点D,C分别为垂足
如图,A(x1,y1),B (x2,y2)是直角坐标系中的任意两点,AD,BC都垂直于x轴,点D,C分别为垂足