题目内容
9.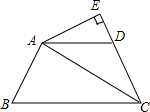 已知四边形ABCD中,AB=AD,CA平分△BCD,AE⊥CD交CD延长线于E.请问线段BC,CE及DE间有何关系?说明理由.
已知四边形ABCD中,AB=AD,CA平分△BCD,AE⊥CD交CD延长线于E.请问线段BC,CE及DE间有何关系?说明理由.
分析 根据角平分线的性质,可得AF与AE的关系,根据全等三角形的判定与性质,可得AF与CE的关系,BF与DE的关系,根据线段的和差,可得BC=BF+CF,再根据等量代换,可得答案.
解答 解:BC=CE+DE,理由如下:
如图: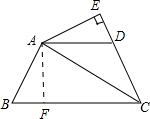 作AF⊥BC于F点,
作AF⊥BC于F点,
∵CA平分△BCD,AE⊥CD交CD延长线于E,AF⊥BC于F点,
∴AF=AE,∠AEC=∠AFC=90°.
在Rt△ACE和Rt△ACF中,
$\left\{\begin{array}{l}{AE=AF}\\{AC=AC}\end{array}\right.$,
∴Rt△ACE≌Rt△ACF (HL),
∴CE=CF.
在Rt△ABF和Rt△ADE中,
$\left\{\begin{array}{l}{AB=AD}\\{AF=AE}\end{array}\right.$,
∴Rt△ABF≌Rt△ADE (HL),
∴BF=DE.
∵BC=BF+CF,
∴BC=DE+CE.
点评 本题考查了全等三角形的判定与性质,利用了“HL”判定全等三角形全等是解题关键,又利用了全等三角形的对应边相等.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
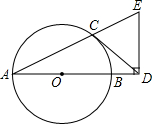 如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.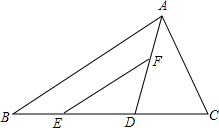 已知,如图△ABC中,AD平分∠BAC,DE=DC,EF∥AB.求证:AC=EF.
已知,如图△ABC中,AD平分∠BAC,DE=DC,EF∥AB.求证:AC=EF.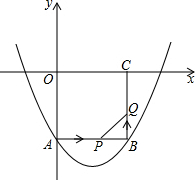 如图,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B和D(4,-$\frac{2}{3}$).
如图,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B和D(4,-$\frac{2}{3}$).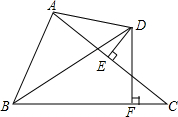 如图,△ABC中,AC的垂直平分线DE交AC于E,交∠ABC的平分线于D,DF⊥BC于F
如图,△ABC中,AC的垂直平分线DE交AC于E,交∠ABC的平分线于D,DF⊥BC于F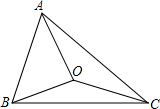 如图,CA=CB,OA=OB,求证:OC⊥AB.
如图,CA=CB,OA=OB,求证:OC⊥AB.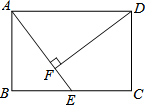 如图,在矩形ABCD中,E是BC边的中点,DF⊥AE,垂足为F.
如图,在矩形ABCD中,E是BC边的中点,DF⊥AE,垂足为F.