题目内容
7.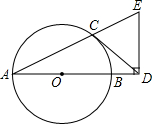 如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.(1)求证:DC=DE;
(2)若tan∠CAB=$\frac{1}{2}$,AB=4,求DC的长.
分析 (1)利用切线的性质结合等腰三角形的性质得出∠DCE=∠E,进而得出答案;
(2)设BD=x,则AD=AB+BD=3+x,OD=OB+BD=1.5+x,利用勾股定理得出BD的长.
解答 (1)证明:连接OC,
∵CD是⊙O的切线,
∴∠OCD=90°,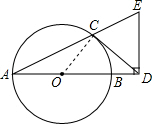
∴∠ACO+∠DCE=90°,
又∵ED⊥AD,
∴∠EDA=90°,
∴∠EAD+∠E=90°,
∵OC=OA,
∴∠ACO=∠EAD,
故∠DCE=∠E,
∴DC=DE;
(2)解:设BD=x,则AD=AB+BD=4+x,OD=OB+BD=2+x,
在Rt△EAD中,
∵tan∠CAB=$\frac{1}{2}$,
∴ED=$\frac{1}{2}$AD=$\frac{1}{2}$(4+x),
由(1)知,DC=$\frac{1}{2}$(4+x),在Rt△OCD中,
OC2+CD2=DO2,
则22+[$\frac{1}{2}$(4+x)]2=(2+x)2,
解得x=$\frac{4}{3}$,
∴CD=$\frac{8}{3}$.
点评 此题主要考查了切线的性质以及以及勾股定理和等腰三角形的性质等知识,熟练应用切线的性质得出∠OCD=90°是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.下列计算正确的是( )
| A. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{27}$$÷\sqrt{3}$=9 | C. | $\sqrt{{4}^{2}+{3}^{2}}$=4+3=7 | D. | $\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$ |
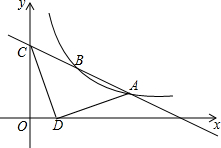 如图,已知一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象相交于A(4,1)、B(a,2)两点,一次函数的图象与y轴的交点为C.
如图,已知一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象相交于A(4,1)、B(a,2)两点,一次函数的图象与y轴的交点为C.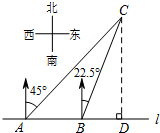 如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为(2+$\sqrt{2}$)km.
如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为(2+$\sqrt{2}$)km. 已知如图,点D在CB延长线上,E在AB上,连接DE,若∠DEB=∠A,点B为DC中点.求证:DE=AC.
已知如图,点D在CB延长线上,E在AB上,连接DE,若∠DEB=∠A,点B为DC中点.求证:DE=AC.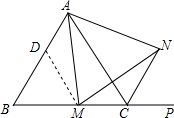 如图,在等边三角形ABC中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点.若∠AMN=60°,求证:AM=MN.
如图,在等边三角形ABC中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点.若∠AMN=60°,求证:AM=MN.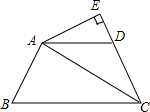 已知四边形ABCD中,AB=AD,CA平分△BCD,AE⊥CD交CD延长线于E.请问线段BC,CE及DE间有何关系?说明理由.
已知四边形ABCD中,AB=AD,CA平分△BCD,AE⊥CD交CD延长线于E.请问线段BC,CE及DE间有何关系?说明理由.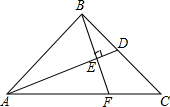 如图,在Rt△ABC中,∠ABC=90°,点D为BC边上的点,BE⊥AD于点E,延长
如图,在Rt△ABC中,∠ABC=90°,点D为BC边上的点,BE⊥AD于点E,延长